- Home
- Schulen
- Lernmaterial
- STEM Electronics
Grundlagen der Elektronik begreifbar machen und nachhaltig verstehen!
Die spannende Welt der Elektronik entdecken mit unserem STEM Electronics! Schritt für Schritt vermittelt dieser Baukasten Grundlagen der Elektronik und bietet eine Vielzahl an verschiedenen Themengebieten der Elektronik. Von einfachen bis hin zu komplexen Modellen, wie beispielsweise Wechselblinker, lassen sich mit diesem Baukasten viele spannende Funktionsmodelle konstruieren. Lehrkräfte finden in unserem e-Learning Bereich Infomaterial zum Thema sowie vorgefertigte Aufgaben und Lösungen.
Nach dem der italienische Physiker Alessandro Graf von Volta im Jahr 1800 die Batterie erfand, stand erstmals eine brauchbare Spannungsquelle zur Verfügung. Die Erforschung der Elektrizität nahm durch die zuverlässige Bereitstellung von Elektrizität richtig Fahrt auf.
1873, ein Dreivierteljahrhundert später, konnte Willoughby Smith die photoelektrischen Eigenschaften von Selen nachweisen. Nur ein Jahr später entdeckte Ferdinand Braun die gleichrichtende Wirkung von Halbleitern. Diese beiden Entdeckungen können als Geburtsstunde der Elektronik gelten.
In der ersten Hälfte des letzten Jahrhunderts war die Elektronenröhre das einzige aktive Bauelement der Elektronik. 1904 stellte John Ambrose Fleming eine Vakuum-Diode vor. Durch das zufügen von Steuergittern in den Elektronenstrom wurden in den folgenden Jahren immer weiter verbesserte Verstärkerröhren verfügbar. Eine Besonderheit dieser Technik waren sicher die Bildröhren (Ferdinand Braun, 1897). Sie wurden für Fernsehgeräte bis in die 2010er Jahre produziert. Ein weiterer besonderer Röhrentyp ist auch heute aus keinem Haushalt wegzudenken: das Magnetron für Mikrowellenherde.
Julius Edgar Lilienfeld ließ sich 1925 ein elektronisches Bauelement patentieren, das mit den heutigen Feldeffekttransistoren vergleichbar ist. Eine praktische Anwendung gelang nicht. Die technischen Voraussetzungen zur Herstellung waren einfach noch nicht gegeben.
John Bardeen, Walter Brattain und William Shockley aus den Bell Laboratories stellten 1947 den ersten Transistor vor und erhielten dafür 9 Jahre später den Nobelpreis für Physik.
In den folgenden Jahren wurde insbesondere die Herstellungstechnik von Transistoren immer weiter verbessert. In den 1950er und 1960er Jahren musste das anfänglich verwendete Germanium dem Silizium weichen. Silizium ist einfacher zu beschaffen, einfacher zu handhaben und damit preiswerter. Zeitgleich hat der Transistor die Röhre immer weiter verdrängt.
Jack Kilby entwickelte 1958 den ersten integrierten Schaltkreis (IC). Es handelte sich um ein FlipFlop aus 2 Transistoren. Heute werden mehr als 50 Milliarden Transistoren auf einem Chip vereinigt. Geschaltet wird mit Geschwindigkeiten im Gigaherz-Bereich.
Ab 1960 leiteten die MOSFETs (Metall-Oxyd-Halbleiter-Feldeffekt-Transistoren) die moderne Leistungselektronik ein. Eine Weiterentwicklung sind die IGBTs (Isolierte-Gate-Bipolar-Transistoren). Sie vereinigen die Eigenschaften von Feldeffekt- und bipolaren Transistoren. Es lassen sich Spannungen über 6000 Volt, Ströme bis weit über 3000 Ampere und Leistungen bis zu 100 Megawatt leistungslos durch geringe Steuerspannungen schalten.
Elektronik hat auch bei fischertechnik Tradition. Bereits 1969 brachten die fischerwerke ihren ersten Elektronik-Baukasten auf den Markt. Ziel war der praxisnahe Einstieg in die Elektronik. Viele weitere Experimentier- und Modellkästen bis hin zum Computing folgten bis heute.
Strom und Spannung
Aufgabe 1
Jede elektronische Schaltung benötigt eine Versorgungsspannung. Diese Spannung wird durch eine Spannungsquelle zur Verfügung gestellt. Die Stärke der Spannungsquelle wird durch die an ihren Polen anliegende Spannung ausgedrückt. Die Spannung ist eine physikalische Größe mit dem Formelzeichen U. Die Höhe der Spannung wird in der Einheit Volt (V) angegeben. Die Spannung der hier verwendeten Batterie im Batteriehalter beträgt 9 Volt.
In der Batterie herrscht durch chemische Prozesse eine Trennung von positiven und negativen Ladungsträgern vor. Die negativen Ladungsträger sind die Elektronen. Positive Ladungsträger sind Stellen von denen die Elektronen verdrängt wurden.
Je mehr Elektronen von ihren Positionen getrennt werden, desto höher die Spannung. Die Spannung ist die Kraft, die die Elektronen zwischen den Polen ausüben. Die Spannung ist zwischen den beiden Polen einer Spannungsquelle messbar.
Wird zwischen den beiden Polen der Batterie ein geschlossener Stromkreis angeschlossen können die Elektronen über den Stromkreis einen Ausgleich herbeiführen. Es fließt ein Strom durch den Stromkreis. Die Spannung treibt den Strom durch den Stromkreis. Je höher die Spannung, desto größer der Strom.
Der Strom hat das Formelzeichen I. Seine Größe wird in Ampere (A) angegeben. In elektronischen Schaltungen sind die fließenden Ströme meist sehr klein. Sie bewegen sich im Milliampere-Bereich (1 mA = 0,001 A). Selbst der verwendete fischertechnik XS-Motor „zieht“ bei normaler Belastung nur etwa 100 mA aus der Spannungsquelle.
Auf den Zusammenhang zwischen Spannung und Strom wird im nächsten Abschnitt genauer eingegangen.
Eine weitere wichtige physikalische Größe ist die Leistung. Ein Stromkreis ist immer eine Folge von Hindernissen für den Strom. An jedem Bauteil (auch Kabel, Stecker, Schalter, …) muss Arbeit verrichtet werden, um das Hindernis zu überwinden. Oft kann die verrichtete Arbeit direkt beobachtet werden. In unserem Stromkreis ist das z.B. das Leuchten der LED. Aber auch die Drehung eines Motors oder die Erwärmung von Bauteilen bedeuten verrichtete Arbeit. Die Arbeit die pro Zeiteinheit verrichtet werden kann ist die Leistung.
Die Leistung kann einfach berechnet werden:
P = U x I Leistung = Spannung x Strom
Elektronische Bauelemente sind empfindlich gegen Temperaturen. Eine starke Erwärmung führt von veränderten Eigenschaften bis hin zur Zerstörung des Bauteils. Daher werden in Datenblättern immer Angaben zur maximalen Verlustleistung gemacht.
Der Widerstand
Aufgabe 4
Der Widerstand ist ein passives Bauteil der Elektrotechnik und Elektronik. Er bewirkt, dass bei einer vorgegebenen Spannung ein bestimmter Strom fließt. Der elektrische Widerstand R ist die physikalische Größe eines Widerstands. Sie wird in Ohm (Ω) angegeben. Die Abhängigkeit von Spannung und Strom an einem elektrischen Widerstand ist proportional und wird durch das Ohm'sche Gesetz ausgedrückt.
R = U / I Widerstand = Spannung / Strom
U = R * I Spannung = Widerstand x Strom
I = U / R Strom = Spannung / Widerstand
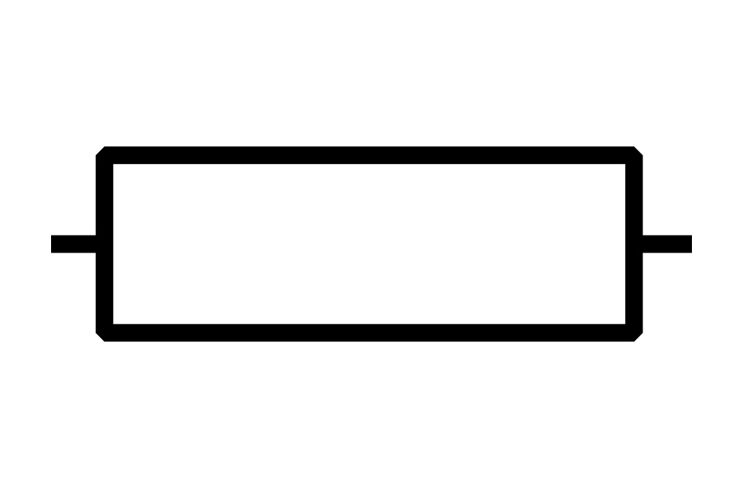
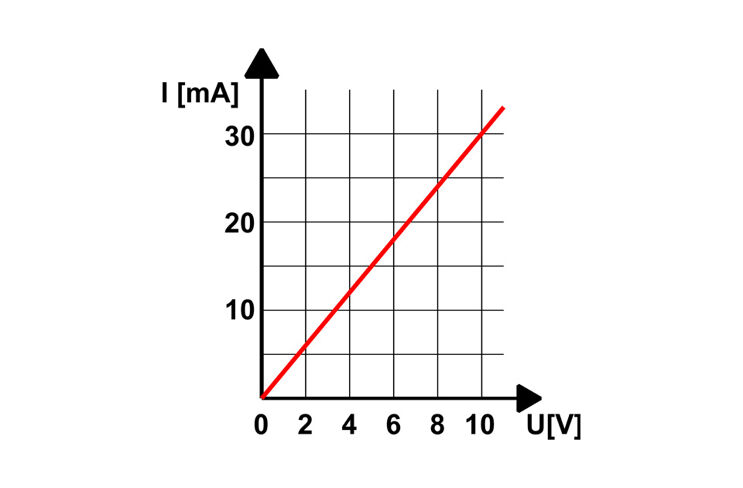
Strom und Spannung in einem Widerstand sind proportional voneinander abhängig. Die Abhängigkeit kann in einer Kennlinie dargestellt werden. In der Abbildung ist die Kennlinie eines 330 Ω Widerstands abgebildet. Bei 9 Volt fließt ein Strom von 0,027 A bzw. 27 mA. Die Kennlinie eines Widerstands ist eine Gerade. Sie ist linear.
Bild Schaltzeichen und Kennlinie
Der elektrische Widerstand eines Bauteils ist immer von Umgebungsbedingungen (z.B. Temperatur) abhängig. In vielen elektronischen Schaltungen sind die Einflüsse so gering, dass sie vernachlässigt werden können. Es gibt Bauteile, bei denen die Einflüsse gezielt ausgenutzt werden. Durch die physikalischen Eigenschaften der verwendeten Materialien reagieren sie z.B. sehr empfindlich auf Licht (LDR = Lichtempfindlicher Widerstand) oder Temperatur (NTC = Heißleiter oder PTC = Kaltleiter).
Die in diesem Kasten verwendeten Widerstände haben die heute gebräuchliche SMD-Bauform (Surface Mounted Device, Bauteil für Oberflächenmontage) und sind aus einem keramischen Träger gefertigt auf den ein Metall- oder Kohlefilm aufgebracht ist. Widerstände lassen sich auch durch Drahtwicklungen oder Halbleitermaterialien realisieren. Letztere finden in integrierten Schaltkreisen Verwendung.
Reihenschaltung von Widerständen
Aufgabe 5
Werden Widerstände in Reihe geschaltet, addieren sich ihre elektrischen Widerstände.
R = R1 + R2 + R3 + …
Gesamtwiderstand = Widerstand 1 + Widerstand 2 + Widerstand 3 + …
Wird eine Spannungsquelle angeschlossen, fällt an jedem Widerstand eine Spannung ab, die proportional zum elektrischen Widerstand ist. Wir sprechen von einem Spannungsteiler. Spannungsteiler sind überall in elektronischen Schaltungen anzutreffen. Erst durch Spannungsteiler ist es möglich, elektronische Bauteile in ihren optimalen Arbeitsbereichen zu betreiben. Man spricht dann von der Einstellung des Arbeitspunktes.
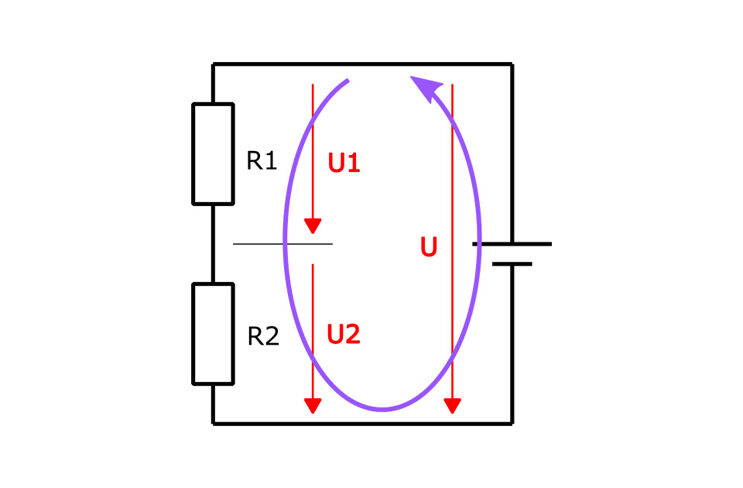
In der Abbildung ist ein Spannungsteiler aus zwei Widerständen dargestellt. Die angelegte Versorgungsspannung U teilt sich an den beiden Widerständen entsprechend ihrer Größe in U1 und U2 auf. Der Zusammenhang kann in einer Formel ausgedrückt werden:
U1/U2=R1/R2
Betrachten wir alle Spannungen im Schaltplan können wir auch den Zusammenhang zwischen der Versorgungsspannung U und den Teilspannungen an den Widerständen erkennen. Da die Spannung U genauso groß ist wie die Gesamtspannung U1 und U2, ergibt sich folgende Formel:
U = U1 + U2
daraus folgt das Verhältnis zur Versorgungsspannung
U/U2=(R1+R2)/R2
Sind die Widerstände bekannt (z.B. R1 = 47 kΩ, R2 = 3,3 kΩ) können wir z.B. U2 berechnen:
U2 = (U x R2)/(R1+ R2) = (9V x 3,3 kΩ)/(47 kΩ + 3,3 kΩ) = 0,59 V
Den Schaltplan in der Abbildung können wir auch als ein Netzwerk aus Spannungen auffassen. Der Zusammenhang wird durch das zweite Kirchhoffsche Gesetz (Maschenregel) ausgedrückt:
Die Summe aller Spannungen in einem Netzwerk ist null.
Die Regel kann mit Hilfe des Richtungspfeils für den Maschenumlauf nachvollzogen werden. Verfolgt man den gesamten Stromkreis bzw. Netzwerk gegen den Uhrzeigersinn wird klar, dass der Richtungspfeil für die Versorgungsspannung U gegen die Umlaufrichtung zeigt. Die Spannung U muss also ein negatives Vorzeichen erhalten. Damit ist die Regel bestätigt:
U1 + U2 – U = 0.
Parallelschaltung von Widerständen
Aufgabe 6
Werden Widerstände parallel geschalten, addieren sich ihre elektrischen Leitwerte (Formelzeichen G). Der Leitwert drückt aus, wie gut ein Material elektrischen Strom leitet. Der Leitwert ist der Kehrwert des elektrischen Widerstands. Mit diesem Wissen kann eine Parallelschaltung von Widerständen berechnet werden.
1/R= 1/R1+1/R2+1/R3+⋯
Der Gesamtwiderstand R ist dabei immer kleiner als der kleinste Widerstand der Parallelschaltung.
Wird eine Spannungsquelle angeschlossen, liegt an allen Widerständen der Parallelschaltung die gleiche Spannung an. Durch jeden Widerstand fließt ein Strom, der umgekehrt proportional zum elektrischen Widerstand ist (proportional zum Leitwert).
In der Abbildung ist eine Parallelschaltung aus zwei Widerständen dargestellt. Der fließende Gesamtstrom I teilt sich an den beiden Widerständen entsprechend ihrer Größe in I1 und I2 auf. Der Zusammenhang kann in einer Formel ausgedrückt werden:
I1/I2=R2/R1
Betrachten wir alle Ströme im Schaltplan können wir auch den Zusammenhang zwischen Gesamtstrom I und den Teilströmen durch die Widerständen erkennen. Da der Gesamtstrom I genau so groß ist wie die Summe der Ströme I1 und I2 ergibt sich folgende Formel:
I = I1 + I2
Sind die Versorgungsspannung und die Widerstände bekannt (z.B. U = 9 V, R1 = 47 kΩ, R2 = 3,3 kΩ) können wir die Ströme mit Hilfe des Ohmschen Gesetzes berechen:
I1 = U/R1 = 9V/(47 kΩ) = 0,19 mA I2 = U/R1 = 9V/(3,3 kΩ) = 2,73 mA
I = I1 + I2 = 0,19mA + 2,73 mA = 2,92 mA
Den Schaltplan in der Abbildung können wir auch als ein Netzwerk aus Strömen auffassen. Der Zusammenhang wird durch das erste Kirchhoffsche Gesetzt (Knotenregel) ausgedrückt:
In einem Knotenpunkt eines Netzwerks ist die Summe aller zufließenden Ströme gleich der Summe aller abfließenden Ströme.
Betrachtet man den im Schaltplan eingezeichneten Knoten fließt I in den Knoten hinein, I1 und I2 aus dem Knoten heraus.
I – I1 – I2 = 0.
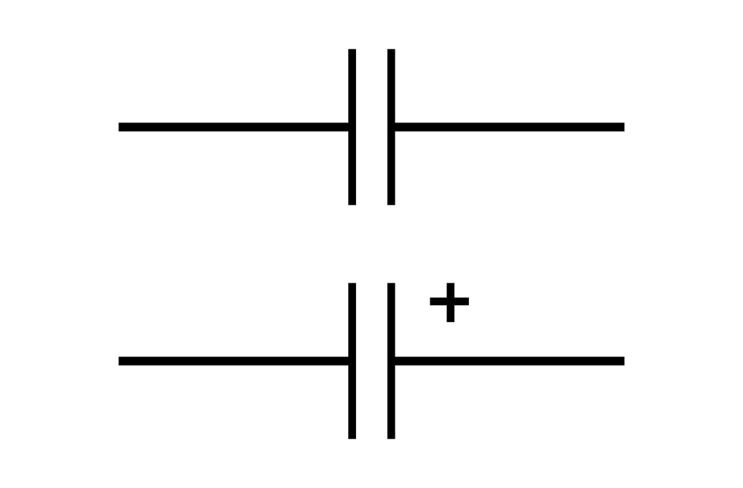
Kondensator
Ein Kondensator kann elektrische Energie speichern. Er besteht prinzipiell aus zwei leitenden Platten, die durch einen Isolator getrennt sind. Der Isolator wird Dielektrikum genannt. Platten und Dielektrikum können aus den unterschiedlichsten Materialien bestehen. Ein Beispiel ist der Folienkondensator. Zwei Kunststofffolien und zwei Metallfolien werden übereinandergelegt und aufgerollt oder gefaltet. Jede Metallfolie erhält einen Anschluss der später aus dem umschließenden Gehäuse ragt.
Eine weitere wichtige Bauform ist der Elektrolytkondensator oder Elko. Das Dielektrikum wird durch eine isolierende Oxydschicht gebildet. Elektrolytkondensatoren sind gepolte Bauelemente. Eine falsche Polung führt zu Zerstörung.
Wird der Kondensator an eine Spannungsquelle angeschlossen, fließen Ladungsträger auf die Platten. Der Kondensator wird aufgeladen. Wird der Kondensator von der Spannungsquelle getrennt, bleibt die Ladung erhalten. Die Ladung gebräuchlicher Kondensatoren ist allerdings so gering, dass sie nicht für den Betrieb elektrischer Verbraucher genutzt werden kann. Eine LED würde nur kurz aufglimmen. In elektronischen Schaltungen fließen sehr geringe Ströme. Hier reicht die Ladung von Kondensatoren für viele Aufgaben aus. Im Experiment zum Kondensator wird dieser langsam über hohe Widerstände entladen, um die Wirkung zu verdeutlichen.
Halbleiter
Moderne Elektronik basiert auf Halbleiterbauelementen. Diese Bauelemente basieren auf hochreinen Halbleiterkristallen. Die Kristalle werden gezielt mit geeigneten Stoffen verunreinigt. Man spricht von Dotieren. In den Kristall werden an den benötigten Stellen weitere Dotierungen mit anderen Stoffen vorgenommen (Umdotieren) um die gewünschten Eigenschaften des Bauelements zu erhalten.
Es gibt zwei Arten von Dotierungen. Durch die n-Dotierung werden Atome in den Kristall eingebaut, die ein Elektron zu viel besitzen (z.B. Phosphor, P). Diese überschüssigen Elektronen können sich frei bewegen. Durch die p-Dotierung werden Atome mit einem Elektron zu wenig eingebaut (z.B. Bor, B). Die Stellen, an denen Elektronen fehlen, werden Löcher oder Defektelektronen genannt. Auch diese Stellen sorgen für die Leitfähigkeit im Kristall. Elektronen können sich von Loch zu Loch bewegen. Die Grenze zwischen p- und n-dotiertem Bereich wird pn-Übergang genannt.
Die Leitfähigkeit des Kristalls steigt durch die Dotierung erst einmal deutlich an. Die Elektronen haben nichts Besseres zu tun als die Löcher zu stopfen. Sie diffundieren in die p-dotierte Zone und rekombinieren mit den Löchern. Die Löcher verschwinden, sie diffundieren scheinbar in die n-dotierte Zone.
Bis in eine gewisse Tiefe (Diffusionslänge) des Materials gelingt das. Der Vorgang kommt schnell zum Erliegen, weil sich durch die Wanderung der Ladungsträger ein elektrisches Feld bildet, das diesem Prozess entgegenwirkt. Es stellt sich ein Gleichgewicht ein. Diese Zone ohne freie Ladungsträger um den pn-Übergang wird als Sperrschicht oder Raumladungszone bezeichnet. Durch die fehlenden Ladungsträger ist ein Stromfluss nicht mehr möglich. Das entstandene elektrische Feld bewirkt die Diffusionsspannung. Sie beträgt für Silizium etwa 0,7 Volt.
Die Diffusionsspannung muss durch Anlegen einer Spannung von außen überschritten werden, damit ein Strom durch den Halbleiter fließen kann. Dabei muss die p-Zone positiver als die n-Zone sein. Das bedeutet, dass die technische Stromrichtung in einem pn-Übergang immer von p nach n verläuft und damit der Bewegungsrichtung der Löcher entspricht. Die Elektronen bewegen sich bei Stromfluss demzufolge von n nach p.
Diode
Aufgaben 7 und 8
Eines der einfachsten Halbleiterbauelemente ist die Diode. Sie besteht aus nur einem pn-Übergang. Gewöhnlich wird in einen n-dotierten Halbleiterkristall an einer Stelle eine p-Dotierung eingebracht. Beide Zonen werden durch Anschlüsse aus dem Gehäuse geführt. Der Anschluss an der p-Zone wird als Anode, der an der n-Zone als Kathode bezeichnet.
Wird eine Siliziumdiode in einem Stromkreis eingesetzt gibt es zwei Möglichkeiten.
Die Anode ist positiver als die Kathode oder umgekehrt. Bei einer um ca. 0,6 – 0,7 Volt positiveren Anodenspannung wird die Diode in Durchlassrichtung betrieben. Die Diffusionsspannung ist abgebaut, Elektronen und Löcher lösen ihre Rekombination auf und wirken als freie Ladungsträger. Es fließt ein Strom.
Im umgekehrten Fall wirken das elektrische Feld der Sperrschicht und die angelegte Spannung in die gleiche Richtung. Das elektrische Feld wird durch die äußere Spannung weiter verstärkt, die Diode sperrt, es kann kein Strom fließen. Die Diode wird in Sperrrichtung betrieben.
Wird die Spannung in Sperrrichtung zu weit erhöht, kommt es durch physikalische Effekte im Halbleiter zu einem ungewollten Durchbruch. Es fließt lawinenartig ein hoher Strom, der die Diode zerstört. Die Durchbruchspannungen der in den Experimenten verwendeten Dioden betragen ca. 700 Volt.
Eine besonderer Typ von Dioden sind die LEDs (Leuchtdioden). Bei Betrieb in Durchlassrichtung wandeln sie elektrische Energie in Licht um. Die Durchlassspannung beträgt je nach Material und Lichtfarbe 1,8 bis 3,7 Volt. Die Sperrspannung liegt meist bei etwa 5 Volt.
Der Transistor
Aufgaben 9 bis 11
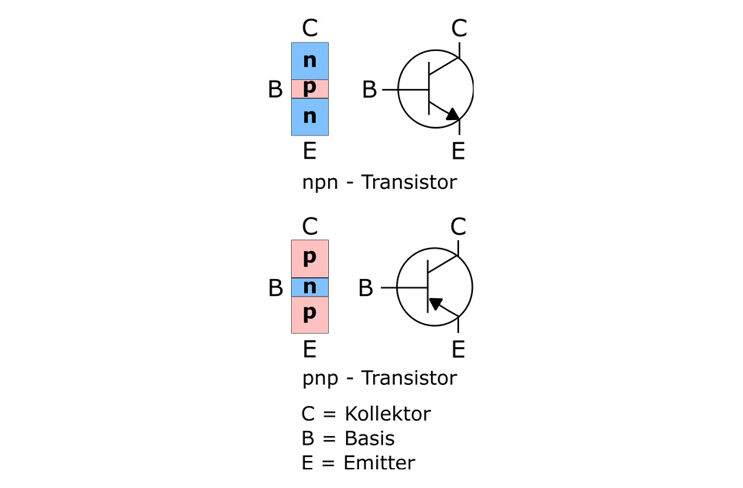
Der „bipolare Transistor“ (BJT) oder einfach Transistor ist ein Halbleiterbauelement mit zwei Sperrschichten. Daraus folgt, dass es zwei pn-Übergänge geben muss. Die Reihenfolge der Dotierung entscheidet über die elektrischen Eigenschaften des Transistors. Die Abbildung zeigt die beiden möglichen Kombinationen.
Wird an einem Transistor zwischen Basis und Emitter eine Spannung angelegt, fließt nach Überschreiten der Diffusionsspannung der Basisstrom IB. Die Strecke verhält sich wie eine Diode. Mit dem Basisstrom gelangen sehr viele Ladungsträger in Basisschicht. Da diese sehr schmal ist müssen immer mehr Ladungsträger in die Sperrschicht zwischen Basis und Kollektor ausweichen. Durch die Ladungsträger wird die Sperrschicht abgebaut und leitend. Es kann ein Kollektorstrom IC fließen. Die Stärke des Stroms ist vom Ladungsträgerangebot in der Basis abhängig. Durch Kollektor und Emitter fließt ein Strom, der vom Basisstrom abhängig ist. Ohne unterstützenden Basisstrom kommt der Vorgang zum Erliegen. Das passiert nicht abrupt, sondern braucht eine kurze Zeit. Die Ladungsträger müssen aus der Basis abfließen. Das ist der Grund warum ein Transistor nicht unendlich schnell schalten kann, er hat eine Grenzfrequenz. Damit sind schnellen Anwendungen, z.B. in Computern, Grenzen gesetzt. Eine weitere Konsequenz: ein Transistor schaltet deutlich schneller ein als aus.
Das Verhältnis zwischen Kollektorstrom IC und Basisstrom IB ist der Stromverstärkungsfaktor B. Er ist ein vom Hersteller bestimmter Parameter. Die Stromverstärkung bewegt sich je nach Transistortyp in einem Bereich von 5 bis 1000. Die Stromverstärkung der in den Experimenten verwendeten Transistoren beträgt etwa 200.
"Verstärkungsfaktor B = " ("Kollektorstrom" "I" _"C" )/("Basisstrom" "I" _"B" )
Der Transistor ist ein Stromverstärker. Wird der Basisstrom erhöht, steigt der Kollektorstrom. Irgendwann wird der Strom durch den Lastwiderstand begrenzt. Auch wenn der Basisstrom erhöht wird, kann der Kollektorstrom nicht weiter steigen. Der Transistor ist voll durchgesteuert. Er wird in Sättigung betrieben. Diese Betriebsart wird verwendet, wenn der Transistor als Schalter verwendet werden soll.
Wird der Transistor als Verstärker verwendet, muss er in einem Bereich betrieben werden, in dem der Kollektorstrom proportional vom Basisstrom abhängig ist.
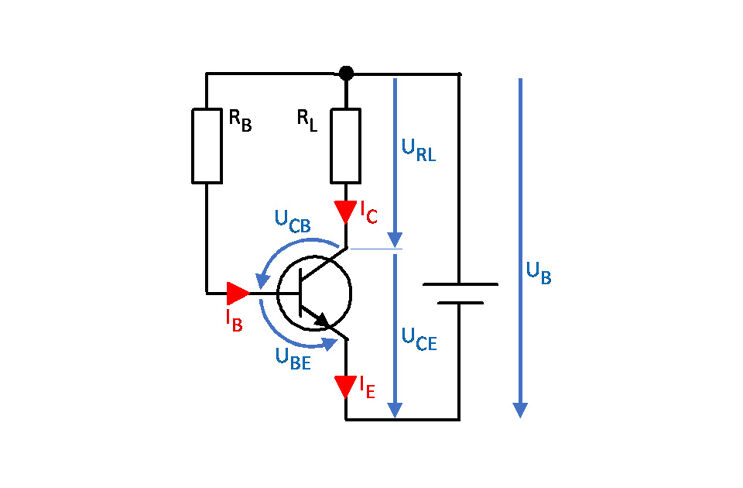
In einer Transistorschaltung sind verschiedene Spannungen und Ströme von Bedeutung. Sie sind in der Abbildung dargestellt.
UB - Versorgungsspannung
UBE - Basis-Emitter-Spannung
IB - Basisstrom
UCE - Kollektor-Emitter-Spannung
IC - Kollektorstrom
RL - Lastwiderstand (z.B. eine Lampe)
RB - Basisvorwiderstand
B - Stromverstärkungsfaktor
UCB und IE sind nur von geringer Bedeutung. Sie können jederzeit aus den anderen Werten berechnet werden.
Es muss dafür gesorgt werden, dass der Transistor innerhalb der Herstellerspezifikationen betrieben wird. Folgende Parameter dürfen nicht überschritten werden:
UCB0 - Maximale Kollektor-Basis-Spannung
UCE0 - Maximale Sperrspannung
UEB0 - Maximale Basis-Emitter-Spannung
IC - Maximaler Kollektorstrom
Ptot - Maximale Verlustleistung (UCE x IC, Basisstrom vernachlässigt)
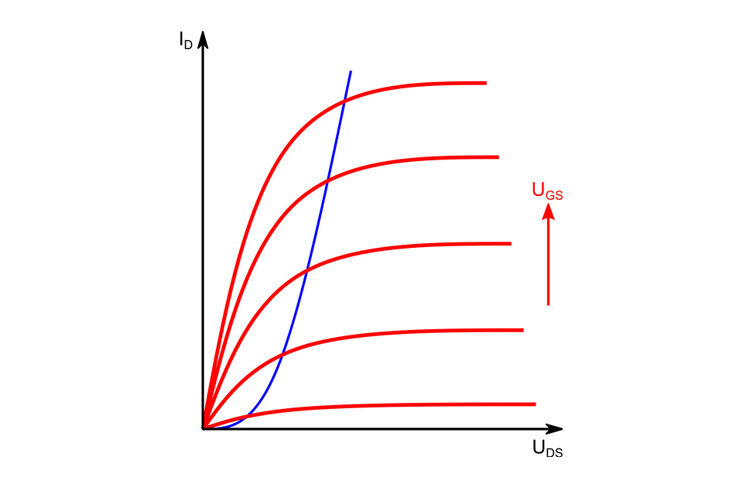
Einige Parameter werden durch Kennlinien dargestellt, um die Abhängigkeit verschiedener Werte voneinander auszudrücken. Die Wichtigste Kennlinie die einen Transistor beschreibt ist die Ausgangskennlinie (Abbildung rechts). Aus ihr kann für verschiedene Basisströme der Zusammenhang zwischen der Kollektor-Emitter-Spannung und dem Kollektorstrom abgelesen werden. Aus der Linie eines Basisstroms kann nach Ablesung des Kollektorstroms auch der Verstärkungsfaktor berechnet werden. Die gelbe Linie gibt den Bereich an, der nicht überschritten werden darf. Das Produkt aus Kollektor-Emitter-Spannung und Kollektorstrom gibt die in Wärme umgesetzte Leistung an. Diese wäre jenseits der Linie zu hoch und würde den Transistor zerstören.
Viele Hersteller geben heute nicht mehr alle Kennlinien an. Für die Berechnung von Schaltungen muss dann auf die im Datenblatt enthaltenen Parameter zurückgegriffen werden. Mit den Angaben aus dem Datenblatt können Transistorschaltungen berechnet werden. Dazu werden nur das Ohmsche Gesetz und die Kirchhoffschen Regeln benötigt.
Steht der Widerstand einer Last (Verbraucher) fest, kann der Strom durch ihn und damit durch den Kollektor bestimmt werden:
UL = UB – UCE, IL = IC = UL / R
Der Basisstrom lässt sich durch einfache Division des Kollektorstroms mit dem Stromverstärkungsfaktor B berechnen:
IB = IC / B
Der benötigte Basisstrom wiederum bestimmt den Basisvorwiderstand. An diesem fällt die Spannung URB ab. Die Spannung entspricht der Versorgungsspannung abzüglich der Diffusionsspannung der Basis-Emitter-Strecke:
URB = UB – 0,7V
Ist diese Spannung bekannt lässt sich der Basisvorwiderstand berechnen:
RB = URB / IB
Die Darlingtonschaltung
Aufgabe 12
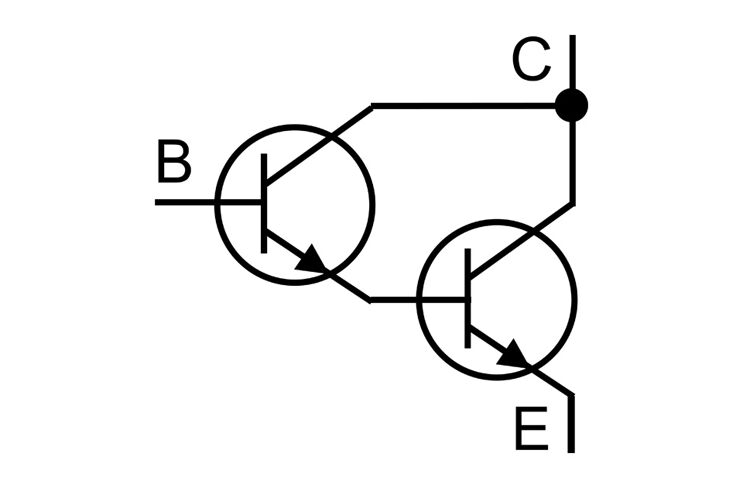
Die Darlingtonschaltung ist eine besondere Zusammenschaltung von zwei Transistoren (siehe Abbildung). Basis- und Kollektorstrom, die über den Emitter aus dem Transistor herausfließen werden direkt als Basisstrom für den zweiten Transistor genutzt. In dieser Schaltung multiplizieren sich die Stromverstärkungsfaktoren der beiden Transistoren.
Bgesamt = BT1 x BT2
Darlingtonschaltungen besitzen sehr hohe Stromverstärkungsfaktoren. Es werden Faktoren über 500.000 erreicht.
Werden Darlingtonschaltungen benötigt, greift man heute direkt auf Darlingtontransistoren zurück. Sie bestehen aus einer Darlingtonschaltung in einem Transistorgehäuse.
MOSFET
metal-oxyde-semiconductor-field-effect-transistor
Aufgaben 13 bis 15
MOSFETs haben Transistoren in vielen Bereichen abgelöst. Insbesondere in der Digital- und Leistungselektronik wird überwiegend auf dieses Bauteil zurückgegriffen. MOSFETs lassen sich sehr effizient in enormen Stückzahlen produzieren und zu Komplexen Schaltkreisen auf einem Stück Silizium zusammenfassen. Es gibt Mikroprozessoren die aus mehr als 50 Mrd. einzelnen MOSFETs bestehen.
In der Leistungselektronik werden durch MOSFETs enorme Ströme bei sehr hohen Spannungen geschaltet. Der Einsatz von mechanischen Leistungsschaltern ist nicht mehr notwendig. Das wird durch die sehr guten elektrischen Eigenschaften moderner MOSFETs möglich.
Im Prinzip ist der MOSFET ein Halbleiterbauelement, das sich wie ein spannungsgesteuerter Widerstand verhält. Im Gegensatz zum bipolaren Transistor fließ kein Steuerstrom. Der MOSFET wird leistungslos gesteuert.
Ein MOSFET besteht aus einem Halbleiterkristall der schwach n- oder p-dotiert sein kann. Es gibt spezielle Typen, die auf einem undotierten Kristall basieren.
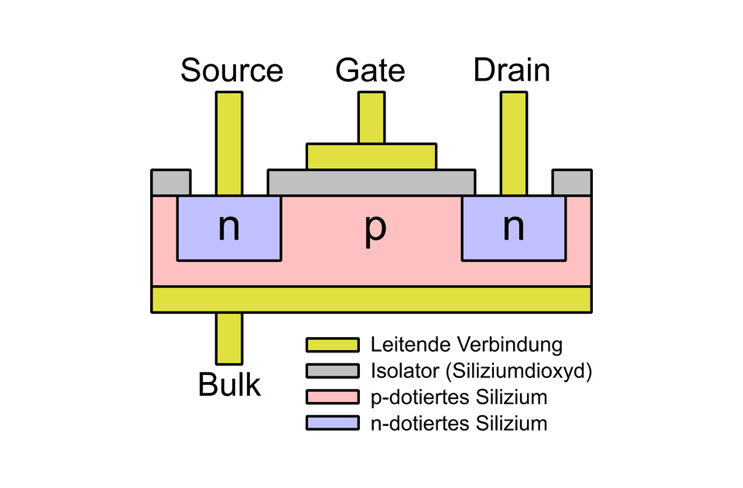
Ein n-Kanal MOSFET, wie er für die Experimente zum Einsatz kommt, besteht aus einem p-dotiertem Silizium (Substrat) in das zwei n-Zonen eingebracht sind (Abbildung links oben). Die beiden Zonen sind mit dem Drain- und Source-Anschluss verbunden. Auf den Bereich zwischen den Zonen ist eine Isolierschicht aufgebracht. Auf der Isolierschicht befindet sich die Gate-Elektrode. Am Substrat befindet sich der Bulk-Anschluss. Dieser ist intern mit dem Source verbunden.
Wird am Gate eine positive Spannung angelegt (Abbildung links unten), werden durch das entstandene elektrische Feld Elektronen angesogen. Das Gate verhält sich zum Substrat wie ein Kondensator. Die angesammelten Elektronen bilden unterhalb der Gate-Elektrode einen Kanal, der sich wie n-dotiertes Silizium verhält. Der Kanal verbindet die beiden n-Zonen miteinander und hebt die Sperrschichten auf. Es kann ein Strom fließen. Der Kanal hat bei modernen MOSFETs einen sehr geringen Widerstand (< 10 mOhm). Die Verlustleistung auch bei großen Strömen kann damit sehr gering gehalten werden.
Der Stromfluss zwischen Drain und Source ist in beide Richtungen möglich. Die Hersteller optimieren die MOSFETs jedoch für die Flussrichtung Drain – Source.
Durch Parallelschaltung mehrerer MOSFET-Zellen auf einem Substrat können Bauelemente realisiert werden, die erhebliche Ströme schalten können (> 3000 Ampere).
Der MOSFET als Schalter
Aufgabe 14 bis 15
MOSFETs für die Leistungselektronik sollen einen möglichst geringen Widerstand RDS(on) des Kanals zwischen Drain und Source haben. Heute werden Werte von einigen Milliohm erreicht.
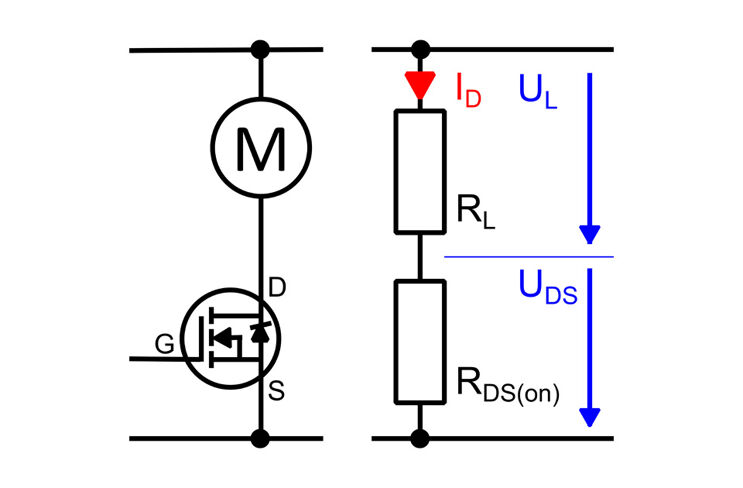
Der Laststrom ID fließt durch Lastwiderstand und Kanal zwischen Drain und Source. Der Kanal ist mit dem Lastwiderstand RL in Reihe geschaltet. In der Abbildung ist der Zusammenhang in unserer Schaltung und als Ersatzschaltbild dargestellt. Das Ziel ist, RDS(on) wesentlich kleiner als RL werden zu lassen. So ist gewährleistet, dass am MOSFET nur ein sehr kleiner Teil der Versorgungsspannung abfällt. Die Leistung die im MOSFET in Wärme umgewandelt wird bleibt gering. Das Bauteil erwärmt sich nicht so stark als dass es zerstört würde.
Es gibt Parameter, die die elektrischen Eigenschaften eines MOSFET beschreiben. Sie sind durch den Herstellungsprozess vorgegeben. Alle Parameter können den Datenblättern der Hersteller entnommen werden.
UBR - Durchbruchspannung der Drain-Source-Strecke.
IDmax- Maximaler Strom der durch die Drain-Source-Strecke fließen darf.
RDS(on) - Widerstand der Drain-Source-Strecke im durchgeschalteten Zustand.
UGSth - Schwellspannung ab der die Drain-Source-Strecke leitet.
Ptot- Maximale Verlustleistung die im Halbleiter in Wärme umgesetzt wird.
Die genannten Parameter reichen in der Leistungselektronik aus um Schaltungen mit MOSFETs zu entwerfen. Der Bereich in dem ein MOSFET arbeiten darf wird von den Parametern begrenzt.
Er darf …
… keine Spannung höher UBR schalten.
… kein Strom größer IDmax fließen.
… darf keine Leistung größer UDS x ID umgesetzt werden.
… kann kein Strom größer UDS / RDS(on) fließen.
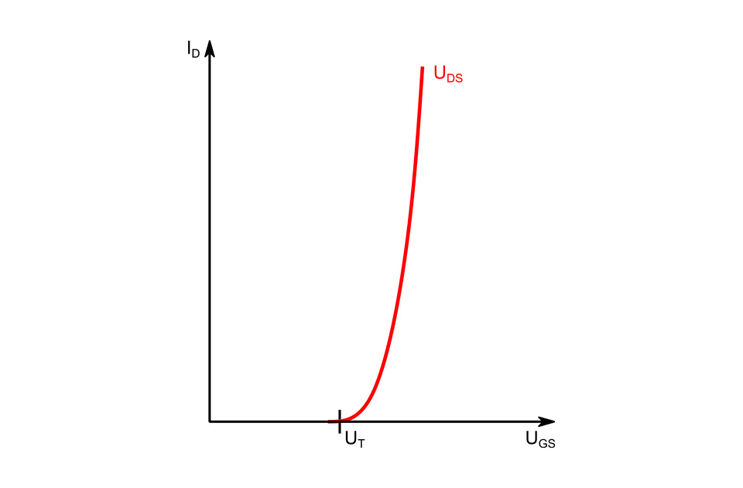
Einige Eigenschaften werden durch die Hersteller in Form von Kennlinien veröffentlicht. Eine dieser Kennlinien ist die Übertragungs- oder Transferkennlinie (Abbildung links oben). Sie sagt aus, welchen Einfluss die Gatespannung UGS auf den Drainstrom ID hat. Typisch ist, dass die Schwellspannung UT überschritten werden muss um überhaupt einen Drainstrom fließen zu lassen.
Wir nutzen die Kennlinie um herauszufinden, wie hoch die Gatespannung sein muss, um den gewünschten Strom durch die Last zuverlässig zu schalten.
Der MOSFET, der in den Experimenten verwendet wird, hat eine besonders niedrige Schwellspannung. Er ist für den direkten Einsatz in Logikschaltungen vorgesehen. Diese arbeiten mit 3 bis 5 Volt.
Eine weitere Kennlinie ist die Ausgangkennlinie (Abbildung links unten). Sie informiert über die Abhängigkeit des Drainstroms ID von der Drain-Source-Spannung UDS für mehrere Gatespannungen UGS.
Im Schaltbetrieb ist der Bereich links der blauen Linie interessant. In diesem Bereich ist der Widerstand der Drain-Source-Strecke am günstigsten.
Die bistabile Kippstufe
Aufgabe 17
Die bistabile Kippstufe oder der bistabile Multivibrator ist eine wichtige elektronische Grundschaltung. Sie stellt prinzipiell eine Speicherstelle für ein Bit dar. Diese Schaltung findet sich zu tausenden in Mikroprozessoren und ist die Grundschaltung für dynamische RAM-Bausteine. Die bistabile Kippstufe wird auch als Flip-Flop bezeichnet.
Bistabile Kippstufen werden heute nur in Ausnahmefällen aus einzelnen Transistoren aufgebaut. Es existiert eine große Auswahl integrierter Schaltkreise die ein oder mehrere dieser Schaltungen enthalten.
In der folgenden Logiktabelle sind die Zusammenhänge zwischen Signalen an den Eingängen sowie den beiden Ausgängen dargestellt. Es handelt sich um die einfachste Form einer bistabilen Kippstufe, das RS Flip-Flop. Der Name ist von den beiden Eingängen abgeleitet.
|
S |
R |
Q1 |
Q2 |
Bemerkung |
|
1 |
0 |
1 |
0 |
Setzen (set) |
|
0 |
0 |
X |
X |
Letzter gespeicherter Zustand |
|
0 |
1 |
0 |
1 |
Löschen (reset) |
|
1 |
1 |
0 |
0 |
Nur solange Signal anliegt, nicht speicherbar |
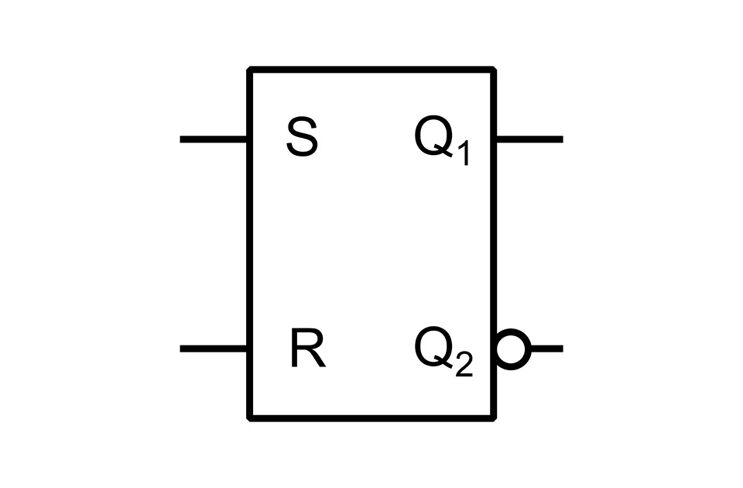
Das Flip-Flop hat häufig zwei Ausgänge. Der zweite Ausgang ist dann negiert. Das heißt, es liegt immer das entgegengesetzte logische Signal an. Die Negation wird durch den kleinen Kreis angedeutet.
Wird einer der beiden Eingänge mit einem logischen Signal angesteuert, wird dieses an den Ausgang weitergeleitet und gespeichert. Liegen danach keine Signale an den Eingängen bleibt dieser Zustand erhalten. Erst ein Signal an Eingang R kann den Ausgang zurücksetzen. Sind beide Eingänge mit Signalen belegt, liegt ein nicht erwünschter Zustand vor. Nach Entfernen der Signale bleibt der Ausgang abhängig von der Reihenfolge des Abschaltens gesetzt oder gelöscht.
Die monostabile Kippstufe
Aufgabe 18
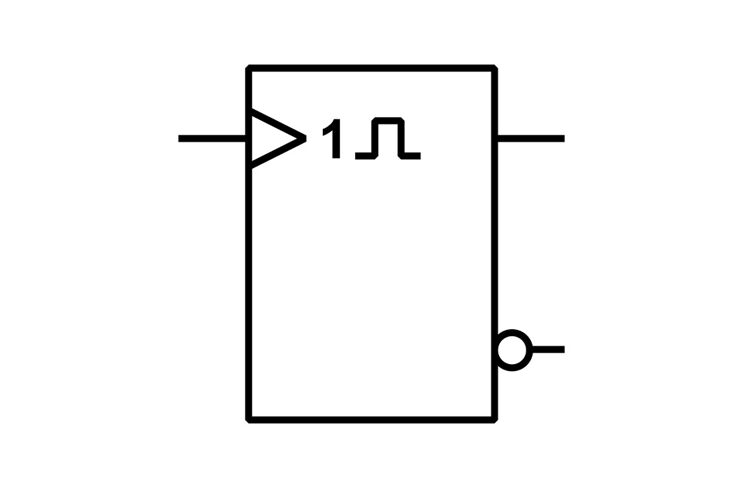
Die monostabile Kippstufe oder monostabiler Multivibrator ist eine elektronische Grundschaltung mit einem Zeitverhalten. Das Zeitverhalten wird durch den Rechteckimpuls im Schaltbild (Abbildung links) dargestellt. Im Schaltbild ist außerdem zu erkennen, dass der Eingang keinen Spannungspegel benötigt sondern durch einen Impuls von 0 nach 1 geschaltet wird. Das bedeutet, der Übergang von 0 (keine Spannung) zu 1 (Spannung liegt an) löst den Schaltvorgang aus. Der Übergang wird als Flanke bezeichnet. Wir sprechen von einem dynamischen Eingang. Das Dreieck im Schaltbild steht für einen dynamischen Eingang. Die monostabile Kippstufe wird auch als Mono-Flop bezeichnet.
Das Mono-Flop hat häufig zwei Ausgänge. Der zweite Ausgang ist dann negiert. Das heißt, es liegt immer das entgegengesetzte logische Signal an. Die Negation wird durch den kleinen Kreis angedeutet.
Wird der Eingang mit einem logischen Signal angesteuert, wird dieses an den Ausgang weitergeleitet und gespeichert. Nach einer vorgegebenen Zeit wechselt der Ausgang selbständig in den Ausgangszustand zurück.
Die Zeitspanne kann durch ein RC-Glied vorgegeben werden. Ein RC-Glied ist eine Zusammenschaltung aus Widerstand (R) und Kondensator (C). Über den Widerstand wird ein Kondensator aufgeladen oder entladen. Für den Vorgang ist eine Zeitspanne erforderlich, die durch folgende Formel berechnet werden kann.
t=ln(2)*R1*C1
Der Logarithmus ln(2) kann durch die Konstante 0,7 ersetzt werden.
Astabile Kippstufe
Aufgabe 19
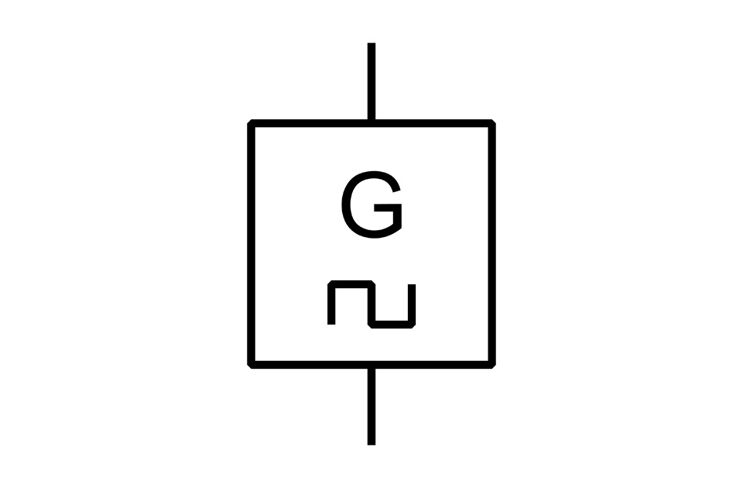
Die astabile Kippstufe bzw. der astabile Multivibrator ist eine elektronische Grundschaltung, die selbstständig periodisch zwischen zwei Zuständen wechselt. Die Schaltzeiten werden durch 2 RC-Glieder bestimmt.
Für die astabile Kippstufe gibt es kein eigenes Schaltzeichen. Sie ist prinzipiell ein Generator mit bestimmter Frequenz. Da die Ausgangsspannung zwischen zwei Werten pendelt ähnelt sie einem Rechteckgenerator.
Für den Durchlauf eines kompletten Zyklus ist eine bestimmte Zeit T erforderlich. Sie ist die Summe der Zeiten der beiden RC-Glieder. Sind beide RC-Glieder identisch dimensioniert sind sie symmetrisch aufgebaut. Dann kann die nachstehende Formel angewandt werden. Die Konstante 2 gibt an, dass 2 identische RC-Glieder vorhanden sind.
T=2*ln(2)*R1*C1≈1,386*R1*C1
In der Praxis wird selten die Periodendauer T angegeben. Wichtiger ist die Anzahl der abgegebenen Impulse pro Zeiteinheit. Die Anzahl der Impulse pro Sekunde ist die Frequenz f. Die Maßeinheit der Frequenz ist das Herz (Hz). Die Frequenz lässt sich mit folgender Formel berechnen:
f=1/T
Der Schmitt-Trigger
Aufgabe 20
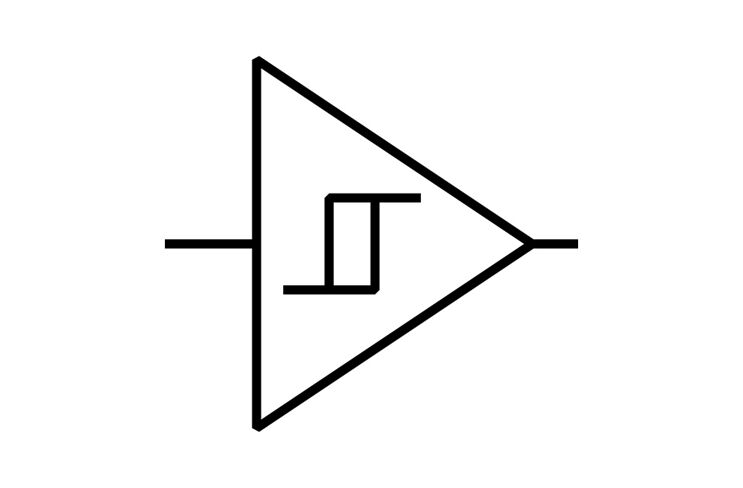
Der Schmitt-Trigger ist eine Kippschaltung, in der eine Eingangsspannung mit einer in der Schaltung vorgegebenen Spannung verglichen wird. Eine Besonderheit des Schmitt-Triggers ist, dass Einschalt- und Ausschaltspannung nicht identisch sind. Die Differenz wird Schalthysterese oder einfach Hysterese genannt.
Die Ausgangsspannung kann nahezu Versorgungsspannung annehmen. Der Schmitt-Trigger eignet sich dazu, beliebige Spannungen in fest definierte logische Ausgangspegel zu wandeln.
Das schlagartige Umschalten der Ausgangsspannung wird durch den gemeinsamen Emitterwiderstand RE erreicht. Durch einen Spannungsabfall der dort entsteht, sobald T1 durch eine Basisspannung durchsteuert, wird auch die Emitterspannung von T2 angehoben. Zeitgleich verringert sich die Basisspannung von T2 da T1 leitet. Die Spannung zwischen Basis und Emitter von T2 verringert sich schlagartig, T2 sperrt, die Schaltung ist gekippt.
Besonders die Eigenschaft, klar definierte Ausgangspegel zu liefern, macht den Schmitt-Trigger zu einer sehr häufig angewandten Schaltung. Jegliche Signale die durch die reale Welt geleitet werden unterliegen störenden Einflüssen. Die Übertragung digitaler Informationen über Satellit oder lange Unterseekabel wäre unmöglich, wenn Schmitt-Trigger nicht für eine Wiederherstellung der ursprünglichen Signale sorgen würden.
Diese Fähigkeit ist in Abbildung links unten dargestellt. Die Spannungsdifferenz die durch die beiden schwarzen waagerechten Linien dargestellt wird ist die Hysterese. Die Einschaltspannung liegt immer oberhalb der Ausschaltspannung.
Der Differenzverstärker
Aufgabe 21
Ein Differenzverstärker ist eine Verstärkerschaltung mit zwei Eingängen. Verstärkt wird die Spannungsdifferenz zwischen den beiden Eingängen. Differenzverstärker werden praktisch nur als vollständige Schaltungen in Form integrierter Schaltkreise angeboten. Von großer Bedeutung sind Operationsverstärker. Auch sie bestehen in der Eingangsbeschaltung aus einem Differenzverstärker. Dieser ist jedoch um viele weitere Transistorstufen erweitert um die gewünschten Eigenschaften zu erzielen.
Differenzverstärker haben sehr große Bedeutung als Operationsverstärker und in der Messtechnik.
Ein einfacher Differenzverstärker besteht aus zwei Transistorverstärkern die über einen gemeinsamen Emitterwiderstand gekoppelt sind. Der Emitterwiderstand soll unabhängig von der Ansteuerung der Transistoren einen konstanten Strom fließen lassen. In industriellen Schaltungen werden sogenannte Konstantstromquellen in die Schaltungen integriert.
