- Home
- Schulen
- Lernmaterial
- STEM Gear Tech
Grundlagen verschiedener Getriebearten in der Sekundarstufe begreifbar machen!
17 spannende Modelle warten auf die Erforschung der Techniker von morgen! Spielerisch lassen sich die Experimente anhand von Modellen wie einer Balkenwaage, einem Scherenhubgetriebe oder eines Scheibenwischers durchführen und die spannende Technik dahinter vermitteln. Natürlich dürfen auch die verschiedensten Getriebearten, wie beispielsweise ein Uhrengetriebe, verschiedene Planetengetriebe oder ein Differentialgetriebe, nicht fehlen. Das Konzept wird durch das online verfügbare und frei zugängliche Begleitmaterial abgerundet.
Getriebe spielen in der Geschichte der Menschheit eine zentrale Rolle. Einfache Getriebe wurden verwendet, um Feuer zu machen, komplexere waren erforderlich, um Bauwerke wie Stonehenge (ca. 3.500 v.Chr.) oder die sieben Weltwunder der Antike, darunter die noch heute zu bewundernden Pyramiden von Gizeh (ca. 2.500 v.Chr.), zu errichten.
Für die Entwicklung der menschlichen Zivilisation waren Getriebe entscheidend: Sie ermöglichten es, große Gebäude zu erbauen, Wasser zu schöpfen oder schwere Gegenstände anzuheben und zu transportieren. Später wurden sie eingesetzt, um Energie zu gewinnen (Treträder, Wasserräder, Windräder, Dampfmaschine), Wasser zu pumpen (Maschine von Marly) oder Fahrzeuge anzutreiben. Eine wichtige Rolle spielten Getriebe auch bei der Messung der Zeit: Erst mit Pendeluhren und feinmechanischen Getrieben gelang es, Uhren zu konstruieren, mit denen die Zeit präziser bestimmt werden konnte als durch die Bestimmung des Sonnenstands.
Heute stecken Getriebe in fast jedem elektrischen Gerät, meist unsichtbar für den Benutzer. Waschmaschine, Spülmaschine, Staubsauger, Nähmaschine, Fahrrad, Aufzug, Fön, Mixer, Kaffeemaschine, Garagentor, Wanduhr, Waage – diese technischen Errungenschaften des täglichen Lebens wären alle ohne Getriebe nicht möglich. Sogar einfachste Werkzeuge wie Korkenzieher oder Flaschenöffner sind Getriebe. Ohne Getriebe würden wir wahrscheinlich noch in Höhlen leben. Und hätten möglicherweise die Dinosaurier nicht überlebt.
Definition
Was genau ist ein Getriebe? Als Getriebe bezeichnen wir ein technisches Bauteil (auch „Maschinenelement“ genannt), mit dem Bewegungsgrößen geändert werden. Was bedeutet das?
Die Bewegung eines Gegenstands (oder „Objekts“) kann durch die Richtung, die Bahn (oder „Lage“), die Geschwindigkeit und die Art (Drehbewegung, Hin- und Her-Bewegung) beschrieben werden. Ein Getriebe ändert eine oder mehrere dieser Eigenschaften, die wir auch Bewegungsgrößen nennen. Jedes Getriebe hat einen „Eingang“, den so genannten Antrieb, an dem beispielsweise eine Kurbel, ein Motor oder ein weiteres Maschinenelement Kraft überträgt, und (mindestens) einen „Ausgang“, den Abtrieb, an dem eine Bewegung oder Kraft an ein weiteres Maschinenelement weitergegeben wird.
Wir machen das einmal an dem wahrscheinlich einfachsten Getriebe überhaupt, dem Hebel, anschaulich.
Ein Hebel besteht aus einem starren Körper (z.B. einem Balken), der an einer Stelle drehbar gelagert ist. Stellt euch eine Wippe auf einem Spielplatz vor – genau das ist ein Hebel. Die beiden Teile des Wippbalkens, die links und rechts der Lagerung herausragen, werden Hebelarm genannt. Einer der Hebelarme ist der Antrieb, der andere der Abtrieb. Wenn ihr euch auf eine Seite der Wippe setzt, bewegt sich euer Hebelarm nach unten und der andere nach oben – eine Wippe (ein Hebel) ändert also die Bewegungsrichtung. Sie ändert auch die Bahn der Bewegung, denn eure Bewegung des einen Hebelarms wird auf das Ende des anderen Hebelarms übertragen. Und der Hebel kann auch die Geschwindigkeit der Bewegung ändern: Wenn euer Hebelarm länger ist als der Hebelarm des Abtriebs, dann legt ihr beim Wippen eine längere Strecke zurück als das Ende des anderen Hebelarms – aber in derselben Zeit. Also verlangsamt sich die Bewegung des Abtriebs.
Dabei passiert etwas Faszinierendes:Die Kraft, die ihr durch euer Gewicht auf den Antriebs-Hebelarm der Wippe ausübt, wird auf den Abtriebs-Hebelarm übertragen. Ist der kürzer als der Antriebs-Hebelarm, vergrößert sich die Kraft! Das habt ihr bestimmt auch schon einmal beobachtet: Wenn auf der einen Seite der Wippe ein größeres Kind sitzt als auf der anderen, dann kann man die Wippe ins Gleichgewicht bringen, indem das größere Kind seinen Hebelarm verkürzt, indem es nach vorne (Richtung Drehgelenk) rutscht. Ein Getriebe kann also noch etwas: Es kann Kraft verstärken.
Einfache Getriebe wie der Hebel oder der Flaschenzug sind den Menschen seit Jahrtausenden bekannt und wurden vor allem zum Heben von Lasten (z. B. bei Bauwerken oder dem Be- und Entladen von Schiffen und Fuhrwerken) eingesetzt.
Die ältesten uns bekannten Aufzeichnungen, in denen Getriebe systematisch untersucht wurden, stammen von den Griechen. So wurde, soweit wir wissen, das „Hebelgesetz“ erstmalig von Archimedes von Syrakus (ca. 287-212 v.Chr.) beschrieben. Die Kraftverstärkung eines Hebels begeisterte ihn so, dass er sich sogar zu dem Ausruf hinreißen ließ: „Gebt mir einen festen Punkt im All, und ich werde die Welt aus den Angeln heben.“
Der römische Architekt und Baumeister Marcus Vitruvius Pollio (Vitruv, ca. 75-15 v.Chr.) verfasste mit seinen (heute noch erhaltenen) „Zehn Büchern über Architektur“ das erste Werk über Architektur überhaupt. Band 10 widmete er dem „Maschinenbau“ und beschrieb darin ausführlich die damals bekannten Maschinen und Getriebe. Dazu zählten der Flaschenzug, das Wellrad, das Tretrad, der Trispastos (ein einfacher Kran), griechische Wasseruhren und die Archimedische Schraube (eine „Schnecke“ zur Wasserförderung). Auch in den Werken des Griechen Heron von Alexandria (wahrscheinlich ein Zeitgenosse von Vitruv) findet man „Automaten“ mit Getrieben, z. B. eine windgetriebene Orgel oder die ersten Zahnräder. Die Römer konstruierten auch Kriegsmaschinen (Wurfmaschinen und Schleudern), in denen Getriebe zum Einsatz kamen.
Eine wichtige Rolle spielten Getriebe ein paar Jahrhunderte später bei der Energiegewinnung. Wasserkraft und Windkraft wurden durch Wasser- und Windräder in eine Drehbewegung umgewandelt. Für Mühlen genügte das; für Steinsägen jedoch musste die Dreh- in eine Hin- und Herbewegung der Säge gewandelt werden. Einen ersten Nachweis für die Existenz solcher Schubkurbel-Getriebe liefert die „Zeichnung“ einer Steinsäge mit Wasserrad auf einem Grabstein aus dem 3. Jahrhundert nach Christus.
Eine Blütezeit erlebten Getriebe in der Renaissance, in der man die „alten Schriften“ der Griechen und Römer wiederentdeckte. Vor allem in den Zeichnungen von Leonardo da Vinci (1452-1519) finden sich zahlreiche Getriebe für Baumaschinen, Kriegsmaschinen und erste Fahrzeuge.
Dem Holländer Christiaan Huygens (1629-1695) verdanken wir die erste Pendeluhr, die 1657 entstand. Das Präzisionsgetriebe erreiche eine für die damalige Zeit unglaubliche Gang¬genauigkeit von wenigen Sekunden pro Tag. Nach der Erfindung der Unruh kamen Taschenuhren in Mode. Mit einer solchen Präzisions-Taschenuhr, die auf einer mehrmonatigen Seefahrt nur vier Sekunden falsch ging, löste John Harrison (1693-1776) im Jahr 1759 das „Längengradproblem“ – die präzise Bestimmung des Längengrads auf hoher See.
Mit der Entwicklung von motorisierten „Automobilen“ bekamen Getriebe im 19. und 20. Jahrhundert eine weitere wichtige Bedeutung. Sie mussten die Antriebskraft des Motors mit einem möglichst hohen Wirkungsgrad auf die Räder übertragen. Dafür benötigten sie Schalt- und Differenzialgetriebe.
Drehmoment und Kraftverstärkung
Am Beispiel der Wippe haben wir gesehen, dass Getriebe auch Kraft verstärken können. Das gilt insbesondere für alle Getriebe, die eine Geschwindigkeitsänderung ins Langsame bewirken – wie Ketten-, Zahnrad-, Riemen- oder Schneckengetriebe.
Diese Eigenschaft folgt direkt aus dem Hebelgesetz: Kraft mal Länge des Kraftarms = Last mal Länge des Lastarms. Das Produkt aus wirkender Kraft F und Länge des Kraftarms r nennt man Drehmoment (M).
Erinnert euch an die Wippe: Bei doppelter Kraft (= doppeltes Gewicht) auf der einen Seite genügt die Hälfte des Kraftarms, um dieselbe Last auf der anderen Seite anzuheben. Im Gleichgewicht sind beide Drehmomente gleich und heben sich auf.
Bei einer Wippe ist die wirkende Kraft auf beiden Seiten dieselbe – die Schwerkraft (oder Erdanziehungskraft). Doch das Hebelgesetz gilt für jede Kraft. Damit lässt sich auch die Kraftübertragung bei einem Zahnradgetriebe erklären: Wird das schwarze Zahnrad in der Abbildung angetrieben, so wirkt eine nach unten (oder, bei umgekehrter Drehrichtung, nach oben) gerichtete Kraft auf die Zähne des roten Zahnrads. Je größer das rote Zahnrad, desto länger der Hebelarm (bezogen auf die Achse des roten Zahnrads) – und desto geringer die zum Antrieb des Zahnrads benötigte Kraft. Dafür muss das schwarze Zahnrad häufiger gedreht werden – und zwar im Verhältnis der Hebellängen, also der Radien r der Zahnräder zueinander. Dieses Verhältnis ist wiederum identisch dem Verhältnis der Zahnradumfänge zueinander (denn für den Umfang U gilt: U = 2 r π).
Man kann leicht nachrechnen, dass das Verhältnis der Umdrehungsgeschwindigkeiten der beiden Zahnradachsen (Antrieb zu Abtrieb) also umgekehrt proportional zur jeweils wirkenden Kraft ist. In unserem Beispiel dreht sich die Achse des schwarzen Zahnrads (10 Zähne) dreimal so schnell wie die des roten Zahnrads (30 Zähne) – dafür wirkt, wenn wir Reibungsverluste vernachlässigen, auf die Achse des roten Zahnrads die dreifache Kraft. Mit einem solchen Zahnradgetriebe können wir also die auf eine Achse wirkende Kraft gezielt verstärken.
Dasselbe gilt für Riemen- und Zahnradgetriebe: Der Kehrwert des Verhältnisses der Radien des antreibenden zum abtreibenden Rad beschreibt die Verlangsamung der Achsumdrehung und zugleich Kraftverstärkung.
Form- und kraftschlüssige Getriebe
Es gibt noch eine weitere wichtige Eigenschaft von Getrieben, nach denen wir die vorgestellten Getriebe unterscheiden können. So werden Zahnrad-, Schnecken- und Kettengetriebe als formschlüssig bezeichnet: Die Getriebeelemente (Zähne, Schnecke, Kettenglieder) greifen dabei fest ineinander. Antrieb und Abtrieb sind dadurch fest miteinander verbunden: Sobald ein Antrieb erfolgt, bewegt sich auch der Abtrieb des Getriebes.
Es gibt aber auch Getriebe, bei denen die Getriebeelemente nicht über ihre Form ineinander greifen, sondern „lose“ miteinander verbunden sind. Dazu zählen zum Beispiel Riemengetriebe: Der Riemen wird lediglich durch die wirkenden Reibungskräfte am „Durchrutschen“ gehindert. Diese Getriebe werden kraftschlüssig genannt. Anders als formschlüssige Getriebe sind bei ihnen An- und Abtrieb nicht fest verbunden: Wenn z.B. die Widerstandskraft am Abtrieb zu groß wird, rutscht der Riemen durch. Damit wird der Antrieb (beispielsweise ein Motor) vor Schäden geschützt – er läuft einfach weiter. Den Punkt, an dem die Widerstandskräfte des Abtriebs die Reibungskräfte der Verbindung übersteigen kann man sogar berechnen.
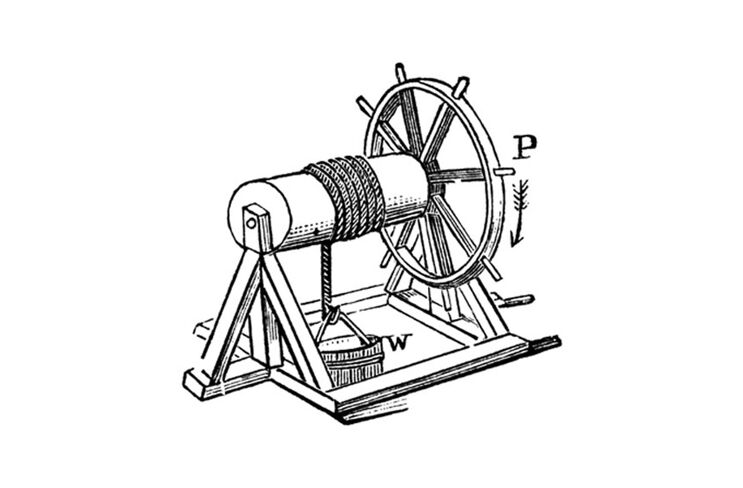
Wellrad
Ein einfaches Getriebe, das sich unmittelbar das Hebelgesetz zu Nutze macht, wurde schon in der Antike eingesetzt: das Wellrad. Dabei wird eine Seilwinde mit mehreren langen Hebeln versehen. Wenn die Hebel die Länge R haben und die Seilwinde den Radius r, dann verstärkt das Wellrad die Kraft des Bedieners der Seilwinde um das Verhältnis der Radien, also den Faktor R/r:
Flaschenzug
Auch ein Flaschenzug, ein weiteres Getriebe, das bereits in der Antike verbreitet war, dient der Kraftverstärkung. Mit ihm kann man die für eine bestimmte Hubarbeit – das Anheben eines bestimmten Gewichts um eine definierte Höhe – erforderliche Kraft über die Länge des zu überwindenden Hubweges steuern.
Die Hubarbeit ist definiert als das Produkt aus Kraft und Weg: Mit einem längeren Hubweg benötigt man daher weniger Kraft für dieselbe Hubarbeit. Ob ihr beispielsweise einen steilen Weg auf eine Anhöhe hinauflauft oder einen flacheren Weg zum Gipfel wählt, leistet ihr dieselbe Hubarbeit (ihr bewegt euer Körpergewicht den Höhenunterschied hinauf). Für den flacheren Weg benötigt ihr für jeden Schritt weniger (Hub-) Kraft – dafür ist der Weg länger.
So ähnlich funktioniert ein Flaschenzug. Er verlängert künstlich den Hubweg, genauer: die Länge des für die Leistung der Hubarbeit aufzuwickelnden Zugseils. Damit ist weniger Kraft für die Hubarbeit erforderlich. Der Preis, den man für diese „Kraftverstärkung“ zahlt: man muss länger ziehen (oder kurbeln). Dabei meinen wir mit „Flaschenzug“ meist einen Faktorenflaschenzug, der die Seillänge durch Seilschlingen und Seilrollen verlängert (siehe Abb.).
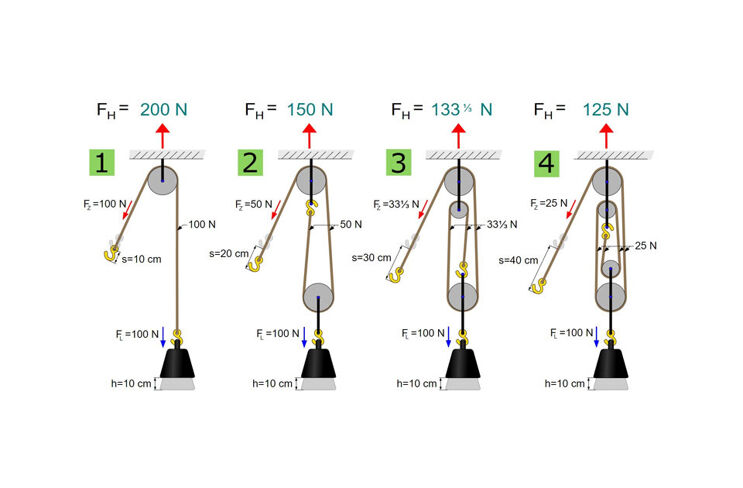
Schon ein einfacher Flaschenzug mit lediglich einer Schlinge verdoppelt die Länge des für den Hub einzuziehenden Zugseils und halbiert damit die dafür benötigte Kraft. Ein Mensch, der maximal 50 kg anheben kann, kann mit einem solchen Flaschenzug mit derselben Zugkraft bis zu 100 kg Last heben. Die Kraftverstärkung lässt sich mit weiteren Seilschlingen vergrößern: Die für die Hubarbeit benötigte Zugkraft FZ sinkt bei n Seilwegen (= Seilrollen) auf ein n-tel der Gewichtskraft FL der Last.
FZ = FL / n
Flaschenzüge haben zudem einen positiven Nebeneffekt: Sie stabilisieren das Zugseil, indem sie Verdrillungen des Seils erschweren: Ein Objekt lässt sich damit sehr gerade nach oben ziehen. Je mehr Seilschlingen, desto widerstandsfähiger ist der Flaschenzug gegen Torsion.
Schließlich wird das Zugseil entlastet, da auf jeden einzelnen Seilstrang nur ein Bruchteil der Gewichtskraft des zu hebenden Gegenstands wirkt. So kann man mit einem Flaschenzug auch sehr schwere Gegenstände mit einem relativ dünnen Seil anheben.
Differentialgetriebe
Eine besonders wichtige Rolle spielt das Differentialgetriebe in der Fahrzeugtechnik. Bei jedem lenkbaren Fahrzeug legen die in Lenkrichtung liegenden „inneren“ Räder einen kürzeren Weg zurück als die „äußeren“. Bei einer Einzelradaufhängung (wie z.B. bei einem Pferdewagen) ist das kein Problem – wohl aber, wenn ein Räderpaar auf einer starren Achse von einem Motor angetrieben wird. Dann kommt es abhängig von der Bodenhaftung bei den inneren Rädern zum Durchdrehen oder bei den äußeren zu „Schlupf“ (Rutschen).
Das kann man vermeiden, indem man nur ein einzelnes Rad antreibt. In der Praxis ist das aber keine befriedigende Lösung. Wesentlich besser funktioniert ein Ausgleichsgetriebe, das den Antrieb bei einer Kurvenfahrt so auf Innen- und Außenrad verteilt, dass beide mit der jeweils passenden Geschwindigkeit angetrieben werden. Genau das leistet ein Differentialgetriebe.
Die Funktionsweise des Differentialgetriebes veranschaulicht man sich am besten, indem man es konstruiert. Der Antrieb wird über ein Z15 auf ein Kronrad (Z32) übertragen. Die vier Kegelzahnräder verteilen die Antriebskraft auf die beiden getrennten Abtriebsachsen (die Räder).
Ist bei einem Rad der Widerstand höher (bspw. bei einer Kurvenfahrt), wird ein Teil der auf diese Achse wirkenden Kraft automatisch so auf die andere Achse „verschoben“, bis die Last ausgeglichen ist.
Und noch eine interessante Eigenschaft hat ein Differentialgetriebe: Dreht man bei angehaltenem Antrieb eines der beiden Achsen (Räder), dreht sich das andere mit derselben Geschwindigkeit in die entgegengesetzte Richtung.
