- Home
- Schools
- Learning material
- STEM Gear Tech
Making the basics of different types of gears understandable at secondary school!
17 exciting models are waiting to be explored by the technicians of tomorrow! Experiments can be carried out in a playful way using models such as a beam balance, a scissor lift gear or a windshield wiper and the exciting technology behind them can be explained. Of course, the various types of gears, such as a clock gear, various planetary gears or a differential gear, are also included. The concept is rounded off by the accompanying material, which is available online and freely accessible.

Gears play a central role in the history of mankind. Simple gears were used to make fire, more complex ones were needed to build structures such as Stonehenge (ca. 3,500 BC) or the seven wonders of the ancient world, including the pyramids of Giza (ca. 2,500 BC), which can still be admired today.
Gears were crucial for the development of human civilization: they made it possible to construct large buildings, draw water or lift and transport heavy objects. Later, they were used to generate energy (pedal wheels, water wheels, windmills, steam engines), pump water (Marly machine) or drive vehicles. Gears also played an important role in measuring time: it was only with pendulum clocks and precision mechanical gears that it was possible to construct clocks with which time could be determined more precisely than by determining the position of the sun.
Today, gears are found in almost every electrical appliance, usually invisible to the user. Washing machines, dishwashers, vacuum cleaners, sewing machines, bicycles, elevators, hair dryers, blenders, coffee machines, garage doors, wall clocks, scales - none of these technical achievements of everyday life would be possible without gears. Even the simplest tools such as corkscrews or bottle openers are gears. Without gears, we would probably still be living in caves. And possibly not have survived the dinosaurs.
Definition
What exactly is a gearbox? A gearbox is a technical component (also known as a "machine element") that is used to change movement variables. What does this mean?
The movement of an object (or "object") can be described by the direction, the path (or "position"), the speed and the type (rotational movement, back and forth movement). A gear changes one or more of these properties, which we also call motion variables. Every gearbox has an "input", the so-called drive, where, for example, a crank, a motor or another machine element transmits force, and (at least) one "output", the output drive, where a movement or force is transmitted to another machine element.

Let's illustrate this using what is probably the simplest transmission of all, the lever.
A lever consists of a rigid body (e.g. a beam) that is pivoted at one point. Imagine a seesaw on a playground - that's exactly what a lever is. The two parts of the seesaw beam that protrude to the left and right of the bearing are called the lever arm. One of the lever arms is the drive, the other is the output. If you sit on one side of the rocker, your lever arm moves downwards and the other upwards - a rocker (a lever) therefore changes the direction of movement. It also changes the path of the movement, because your movement of one lever arm is transferred to the end of the other lever arm. And the lever can also change the speed of the movement: If your lever arm is longer than the lever arm of the output, then you will cover a longer distance than the end of the other lever arm when rocking - but in the same amount of time. So the movement of the output slows down.
Something fascinating happens: The force that you exert on the drive lever arm of the seesaw with your weight is transferred to the output lever arm. If this is shorter than the drive lever arm, the force increases! You have probably observed this before: If a larger child is sitting on one side of the seesaw than on the other, the seesaw can be balanced by the larger child shortening its lever arm by sliding forwards (towards the pivot joint). So a gearbox can do something else: it can amplify force.
Simple gears such as the lever or pulley have been known to man for thousands of years and were mainly used to lift loads (e.g. in buildings or for loading and unloading ships and carts).
The oldest known records in which gears were systematically studied date back to the Greeks. As far as we know, the "law of the lever" was first described by Archimedes of Syracuse (approx. 287-212 BC). He was so enthusiastic about increasing the force of a lever that he even exclaimed: "Give me a fixed point in space and I will unhinge the world."
The Roman architect and master builder Marcus Vitruvius Pollio (Vitruvius, ca. 75-15 BC) wrote the first ever work on architecture with his "Ten Books on Architecture" (still extant today). He dedicated volume 10 to "Mechanical Engineering" and described in detail the machines and gears known at the time. These included the pulley block, the corrugated wheel, the treadwheel, the trispastos (a simple crane), Greek water clocks and the Archimedean screw (a "screw" for pumping water). The works of the Greek Heron of Alexandria (probably a contemporary of Vitruvius) also contain "automata" with gears, e.g. a wind-driven organ or the first cogwheels. The Romans also constructed war machines (throwing machines and slingshots) in which gears were used.
A few centuries later, gears played an important role in energy generation. Water power and wind power were converted into rotary motion by water and wind wheels. This was sufficient for mills; for stone saws, however, the rotary motion had to be converted into a reciprocating motion of the saw. The first evidence for the existence of such slider-crank gears is provided by the "drawing" of a stone saw with a water wheel on a tombstone from the 3rd century AD.

Gears experienced a heyday during the Renaissance, when the "ancient writings" of the Greeks and Romans were rediscovered. The drawings of Leonardo da Vinci (1452-1519) in particular contain numerous gears for construction machinery, war machines and the first vehicles.
We have the Dutchman Christiaan Huygens (1629-1695) to thank for the first pendulum clock, which was created in 1657. The precision gearing achieved a rate accuracy of a few seconds per day, which was unbelievable for the time. After the invention of the balance wheel, pocket watches became fashionable. In 1759, John Harrison (1693-1776) solved the "longitude problem" - the precise determination of longitude on the high seas - with such a precision pocket watch, which was only four seconds wrong on a sea voyage lasting several months.
With the development of motorized "automobiles", gearboxes became even more important in the 19th and 20th centuries. They had to transfer the engine's drive power to the wheels with the highest possible efficiency. To do this, they needed manual and differential gearboxes.

Torque and force amplification
Using the example of the seesaw, we have seen that gears can also amplify force. This applies in particular to all gears that cause a change in speed to a slower speed - such as chain, gear, belt or worm gears.
This property follows directly from the lever law: force times length of force arm = load times length of load arm. The product of the acting force F and the length of the force arm r is called torque (M).

Remember the seesaw: with double the force (= double the weight) on one side, half of the force arm is sufficient to lift the same load on the other side. In equilibrium, both torques are equal and cancel each other out.
In the case of a seesaw, the force acting on both sides is the same - gravity (or the force of gravity). However, the law of leverage applies to any force. This also explains the transmission of force in a gear transmission: If the black gear wheel in the illustration is driven, a force directed downwards (or, if the direction of rotation is reversed, upwards) acts on the teeth of the red gear wheel. The larger the red gear wheel, the longer the lever arm (in relation to the axis of the red gear wheel) - and the lower the force required to drive the gear wheel. To achieve this, the black gear wheel must be turned more frequently - in the ratio of the lever lengths, i.e. the radii r of the gear wheels to each other. This ratio is in turn identical to the ratio of the circumferences of the gears to each other (because the following applies to the circumference U: U = 2 r π).
It is easy to calculate that the ratio of the rotational speeds of the two gear axles (input to output) is therefore inversely proportional to the force acting in each case. In our example, the axis of the black gearwheel (10 teeth) rotates three times as fast as that of the red gearwheel (30 teeth) - but if we neglect friction losses, three times the force acts on the axis of the red gearwheel. With such a gear transmission, we can therefore specifically increase the force acting on an axle.
The same applies to belt and gear drives: The reciprocal value of the ratio of the radii of the driving wheel to the driven wheel describes the deceleration of the axle rotation and at the same time the force amplification.

Positive and non-positive gears
There is another important characteristic of gearboxes according to which we can differentiate between the gearboxes presented. Gear, worm and chain gearboxes are described as positive-locking: The gear elements (teeth, worm, chain links) engage firmly with each other. The drive and output are thus firmly connected to each other: As soon as an input occurs, the output of the gearbox also moves.
However, there are also gearboxes in which the gearbox elements do not interlock via their shape, but are "loosely" connected to each other. These include belt transmissions, for example: the belt is only prevented from "slipping through" by the frictional forces acting on it. These gears are called friction-locked. Unlike form-fit gears, the input and output are not firmly connected: If, for example, the resistance force at the output becomes too great, the belt slips. This protects the drive (e.g. a motor) from damage - it simply continues to run. The point at which the resistance forces of the output exceed the frictional forces of the connection can even be calculated.
Wave wheel
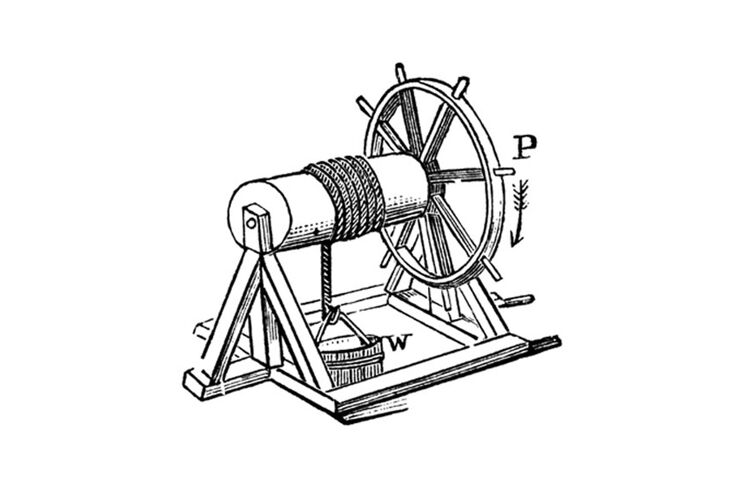
A simple transmission that makes direct use of the law of levers was already used in ancient times: the corrugated wheel. A cable winch is equipped with several long levers. If the levers have the length R and the cable winch has the radius r, then the corrugated wheel increases the force of the operator of the cable winch by the ratio of the radii, i.e. the factor R/r:
Pulley block
A pulley block, another transmission that was already widespread in ancient times, is also used to increase force. It can be used to control the force required for a specific lifting task - lifting a certain weight by a defined height - via the length of the lifting distance to be overcome.
The lifting work is defined as the product of force and distance: with a longer lifting distance, you therefore need less force for the same lifting work. For example, whether you run up a steep path to a hill or choose a flatter path to the summit, you do the same lifting work (you move your body weight up the difference in height). For the flatter path, you need less (lifting) force for each step - but the path is longer.
A pulley works in a similar way. It artificially lengthens the lifting distance, or more precisely: the length of the pull rope to be wound up for the lifting work. This means that less force is required for the lifting work. The price you pay for this "increase in force" is that you have to pull (or crank) longer. By "pulley block" we usually mean a factor pulley block that extends the rope length by means of rope slings and rope pulleys (see illustration).
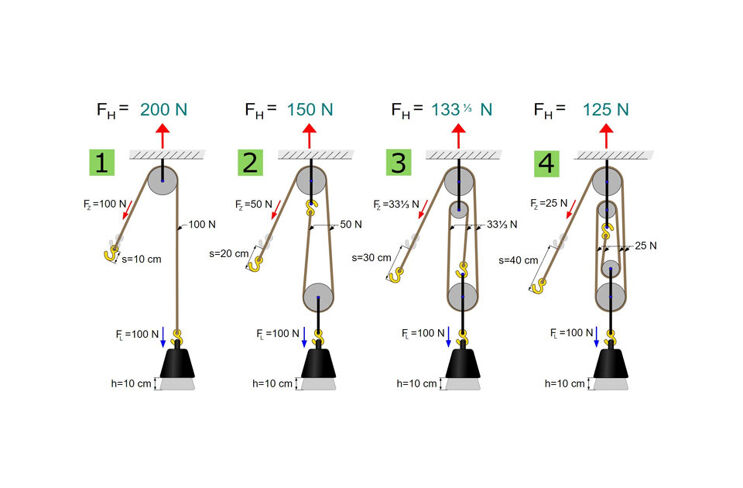
Even a simple pulley block with just one sling doubles the length of the rope to be pulled in for the lift, halving the force required. A person who can lift a maximum of 50 kg can lift a load of up to 100 kg with the same pulling force using such a pulley block. The increase in force can be increased with additional rope slings: The tensile force FZ required for the lifting work drops to one nth of the weight FL of the load with n rope paths (= rope pulleys).
FZ = FL / n
Pulley blocks also have a positive side effect: they stabilize the traction rope by making it more difficult to twist the rope: This allows an object to be pulled very straight upwards. The more rope slings, the more resistant the pulley block is to torsion.
Finally, the load on the pulling rope is reduced, as only a fraction of the weight of the object to be lifted acts on each individual rope strand. This means that even very heavy objects can be lifted with a pulley block using a relatively thin rope.

Differential gearbox
The differential gear plays a particularly important role in vehicle technology. In every steerable vehicle, the "inner" wheels in the steering direction travel a shorter distance than the "outer" wheels. This is not a problem with independent wheel suspension (such as on a horse-drawn carriage) - but it is when a pair of wheels on a rigid axle is driven by an engine. Depending on the road grip, the inner wheels will spin or the outer wheels will slip.
This can be avoided by only driving a single wheel. In practice, however, this is not a satisfactory solution. A differential gear works much better, distributing the drive to the inner and outer wheels when cornering so that both are driven at the appropriate speed. This is exactly what a differential gear does.
The best way to visualize how the differential gear works is to construct it. The drive is transmitted via a Z15 to a crown wheel (Z32). The four bevel gears distribute the drive force to the two separate output axles (the wheels).
If the resistance is higher on one wheel (e.g. when cornering), part of the force acting on this axle is automatically "shifted" to the other axle until the load is balanced.
A differential gear also has another interesting property: if you turn one of the two axles (wheels) when the drive is stopped, the other turns in the opposite direction at the same speed.




