¡Haz que los fundamentos de la robótica sean comprensibles y sostenibles!
El fischertechnik Robotics TXT 4.0 Base Set es el comienzo perfecto para programar como los profesionales. Además de la cámara con procesamiento de imágenes, el completo kit de construcción contiene un sensor ultrasónico, dos motores codificadores, un sensor de orugas, un fototransistor, así como dos botones y dos LED. Los modelos pueden programarse y controlarse con el software de programación gráfica ROBO Pro Coding y el controlador ROBOTICS TXT 4.0. Los principiantes pueden utilizar programas de ejemplo ya preparados, mientras que los usuarios avanzados y profesionales pueden empezar directamente en un entorno de programación Blockly o en Python. Se incluyen 12 apasionantes modelos, desde semáforos peatonales hasta una barrera, un escáner de códigos de barras y robots móviles de conducción con motores codificadores, cámara y sensores de carril y distancia. Además de información introductoria y básica, el completo material didáctico incluye 20 experimentos con soluciones para los 12 modelos.
¿Cómo se programa un microcontrolador?
Por lo general, el microcontrolador no se programa en el propio microcontrolador, sino en un entorno de programación o desarrollo especial (entorno de desarrollo integrado, IDE) en un PC, portátil, tableta o incluso un smartphone. Los programas creados de este modo se transfieren a la memoria del microcontrolador a través de una interfaz de comunicación, por ejemplo USB, WLAN o Bluetooth, y se ejecutan allí.
Así es exactamente como se programa el TXT 4.0: Los programas se desarrollan en ROBO Pro Coding en un PC, portátil o tableta en el lenguaje de programación Blockly o Python y luego se transfieren a la TXT 4.0, en la que se ejecutan.
¿Qué es un "autómata finito"?
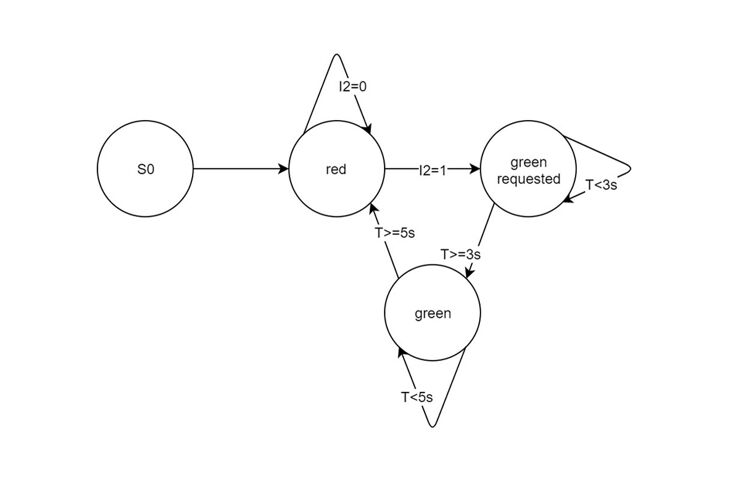
Un "autómata finito" es un sistema cuyo comportamiento puede describirse como un conjunto finito de estados. La transición de un estado a otro se desencadena por condiciones (como sucesos, por ejemplo, cambios en los valores de los sensores), a cada una de las cuales sigue una acción. Por eso, los autómatas finitos también se denominan "máquinas de estados" y se describen mediante diagramas de transición de estados.
Los autómatas finitos desempeñan un papel importante en la descripción de microcontroladores: casi todos los sistemas embebidos (como un controlador de ascensor o un robot) pueden entenderse como un sistema formado por un número finito de estados. La representación como diagrama de transición de estados suele simplificar considerablemente la comprensión del sistema y facilita la programación (sobre todo, sin errores). Esto se debe a que en cada estado sólo hay que tener en cuenta los sucesos que conducen a un cambio de estado, como la solicitud de una señal "verde" en un semáforo peatonal (véase el ejemplo de la ilustración).
¿Qué son los datos analógicos y digitales?
Los microcontroladores sólo pueden procesar estados "on" y "off", es decir, valores binarios que pueden asumir dos estados diferentes. Por eso es muy fácil analizar sensores que también sólo conocen dos estados, como pulsadores, contactos de láminas (interruptores magnéticos) o fototransistores, y el estado del sensor puede almacenarse como dato digital en un bit.
Pero en la realidad, por supuesto, no sólo hay estados binarios. Por ejemplo, la luminosidad, la temperatura o las distancias pueden adoptar muchos valores diferentes. También podemos medir esos datos analógicos con sensores, como una fotorresistencia, un termistor o un sensor de distancia por ultrasonidos. Sin embargo, para que nuestro microcontrolador pueda procesar estos valores analógicos, debe convertirlos en números, es decir, en datos digitales. Sin embargo, se trata de valores más complejos que los valores binarios proporcionados por los sensores digitales: A partir de los estados binarios, el microprocesador puede representar todos los valores numéricos utilizando el sistema dual (y también otros caracteres, como letras, utilizando una codificación adecuada, pero sobre esto hablaremos más adelante).
El valor analógico del sensor se convierte en un número (es decir, en un dato digital más complejo) en un microcontrolador mediante un convertidor analógico-digital (A/D): para ello, el valor del sensor aplicado, normalmente una resistencia eléctrica o una tensión, se "escanea" electrónicamente. Si la resistencia o la tensión son altas, el convertidor A/D entrega un valor numérico grande; si el valor analógico aplicado es bajo, el valor numérico entregado al microcontrolador es pequeño. La precisión con la que puede determinarse el valor analógico presente en la entrada depende de la resolución del convertidor A/D. Ésta suele especificarse en la longitud de bits. Ésta suele especificarse en la longitud en bits del valor resultante.
Las ocho entradas del controlador TXT 4.0 pueden utilizarse tanto como entradas digitales (binarias) como analógicas. Los convertidores A/D de las entradas muestrean valores analógicos como la resistencia eléctrica del termistor, que cambia en función de la temperatura, con una precisión de 12 bits, es decir, convierten la resistencia en un número entre 0 y 4096. Gracias a las diferentes tensiones de referencia, el TXT 4.0 no sólo puede determinar con precisión resistencias en el rango de medición de 5 kOhmios, sino también valores de resistencia notablemente superiores.
¿Qué es la concurrencia?
¿Cómo se determina la temperatura con un termistor?
Un termistor (también conocido como termistor o resistencia NTC) es una resistencia cuyo valor de resistencia cambia en función de la temperatura. Los termistores tienen un coeficiente de temperatura negativo (NTC), es decir, el valor de la resistencia disminuye a medida que aumenta la temperatura. El siguiente diagrama muestra la característica de resistencia del termistor fischertechnik.
El termistor fischertechnik tiene un valor de resistencia de 1,5 kOhmios a 25°C. Como puede observarse en el gráfico, la curva característica del termistor no es lineal. Sin embargo, se puede aproximar el valor de temperatura de forma razonablemente precisa utilizando una curva lineal. Para ello hay que determinar un segundo valor de medición y calcular a partir de él la ecuación de la función lineal.
El termistor fischertechnik tiene un valor de resistencia de 1,5 kOhmios a 25°C. Como puede observarse en el gráfico, la curva característica del termistor no es lineal. Sin embargo, se puede aproximar el valor de temperatura de forma razonablemente precisa utilizando una curva lineal. Para ello, debe determinarse un segundo valor medido y calcular a partir de él la ecuación de la función lineal.
Para un cálculo más preciso del valor de temperatura T (en Kelvin) a partir del valor de resistencia R de una resistencia NTC, se suele utilizar la siguiente ecuación de Steinhart-Hart:
1/T=a+b(lnR)+c(lnR)³.
La temperatura en °C se obtiene a partir de T restando 273,15.
Con dos valores medidos adicionales (además del valor de resistencia de 1,5 kOhmios a 25 °C), podemos establecer un sistema de ecuaciones con las tres incógnitas a, b y c. No tenemos que resolver este sistema de ecuaciones nosotros mismos. No tenemos que resolver este sistema de ecuaciones nosotros mismos: En la página web de Stanford Research Systems hay una "Calculadora de termistores" que calcula los parámetros de la ecuación de Steinhart-Hart que buscamos a partir de los tres valores medidos.
¿Cómo funciona el sensor ultrasónico?
La distancia se mide emitiendo varias señales de 40 kHz de 200 µs de duración (en el espectro inaudible para el ser humano) y midiendo el tiempo que tarda en recibirse su eco, es decir, las ondas sonoras reflejadas por un objeto. La distancia puede calcularse de la siguiente manera a partir del tiempo de propagación de la señal de eco utilizando la velocidad del sonido. Para la velocidad del sonido (en el aire) se aplica lo siguiente
c = (331,5+0,6∙t/°C) m/s
A temperatura ambiente (t=20°C), c es por tanto de unos 343,5 m/s o 0,03435 cm/µs. Para obtener la distancia en cm a partir del tiempo de propagación de la señal (en µs), primero hay que dividirlo por dos y luego multiplicarlo por 0,03435 - o dividirlo por 58,224. Este trabajo lo realiza un circuito integrado en el sensor de ultrasonidos y proporciona la distancia en cm; el sensor también compensa automáticamente la influencia de la temperatura en la medición.
El alcance del sensor ultrasónico es de unos 4 metros. Por lo tanto, a temperatura ambiente, el eco de la señal de disparo tarda 400 ∙ 58,224 = 23,3 ms en volver desde un objeto situado a 4 m de distancia. Si ningún eco llega al sensor durante este tiempo, devuelve el valor "0" (ningún objeto dentro del alcance). El retardo causado por el tiempo de propagación de la señal debe tenerse en cuenta en el sistema de control de un sistema móvil (como un vehículo).
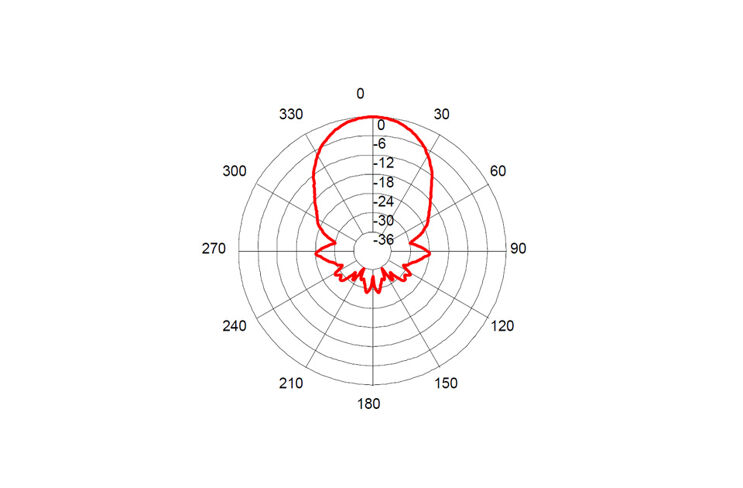
Las ondas sonoras se propagan en círculo, por lo que el sensor tiene un cierto grado de dispersión. Esto significa que no sólo reconoce los obstáculos situados directamente delante de él, sino también los objetos situados a los lados (véase la ilustración).
Por último, es importante tener en cuenta que los ecos sólo llegan al sensor si las ondas sonoras inciden en el objeto con un ángulo no demasiado agudo. Esto se puede comprobar fácilmente de forma experimental.
¿Qué es un código?
Un código es -en términos muy generales- un acuerdo sobre la representación inequívoca de determinada información. Los códigos son necesarios para la transmisión, pero también para la visualización de la información. A cada carácter de un código se le asigna un significado específico. Los códigos que encontramos a diario son, por ejemplo, los números (arábigos) para representar cifras o el lenguaje escrito para representar palabras y frases. Otros códigos son las notas de los pentagramas para representar el tono y la duración de los tonos o los símbolos de los circuitos para representar los componentes electrónicos. Cuando una persona quiere documentar información para otra o intercambiar información entre sí, necesita un código que tanto el emisor como el receptor reconozcan.
Sin embargo, los códigos no sólo desempeñan un papel importante entre las personas: los ordenadores no pueden intercambiar información sin códigos, ni con las personas ni entre sí. Los códigos que utilizan o entienden los ordenadores deben ser especialmente claros e inequívocos para evitar malentendidos. Por esta razón, muchos códigos se diseñan de forma que puedan reconocerse los errores, por ejemplo, causados por un fallo durante la transmisión. Incluso hay códigos que reconocen errores y pueden corregirlos.
¿Cómo se comunican los ordenadores?
¿Cómo funcionan los códigos de barras?
Un código de barras es un "código de barras" formado por barras verticales blancas y negras de diferentes anchuras. Los códigos de barras son códigos unidimensionales, ya que la información está contenida únicamente en la anchura de las barras (por ejemplo, barra estrecha = "0", barra ancha = "1"). El color de las barras (b/n) sólo sirve para diferenciarlas. Los códigos de barras son "códigos ópticos", es decir, pueden ser leídos por un sensor capaz de distinguir entre "claro" y "oscuro" o por una cámara con evaluación de imagen. Los códigos de barras se utilizan principalmente para etiquetar objetos; se encuentran, por ejemplo, en libros y revistas (ISBN/ISSN), en etiquetas de productos o en pegatinas para paquetes postales. Hay muchos códigos de barras diferentes, que se diferencian por la densidad de su información y los dígitos de control utilizados. Los códigos de barras tienen la ventaja de ser muy robustos y fáciles de leer; además, los lectores son muy baratos.
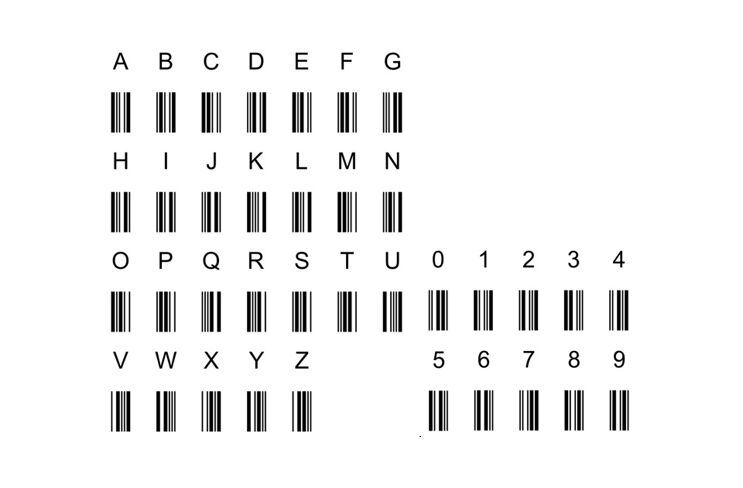
Un código de barras típico es el Código 39, desarrollado por Intermec en 1973 y definido desde entonces por varias organizaciones de normalización (como ANSI e ISO) en especificaciones y normas (como ISO/IEC 16388). Un carácter del Código 39 consta de nueve barras -cinco negras y cuatro blancas (los espacios intermedios)- de dos anchos diferentes. Una barra ancha representa un "1" y una barra estrecha un "0"; por tanto, un carácter Código 39 corresponde a un número binario de nueve dígitos.
Hay un espacio en blanco (estrecho) antes y después de cada carácter para que puedan distinguirse los caracteres individuales. Los códigos de barras Código 39 tienen siempre la misma anchura porque el número de barras anchas por carácter es exactamente tres: dos negras y una blanca. Por lo tanto, un carácter del Código 39 siempre consta de seis barras estrechas y tres anchas, o seis "0" y tres "1". La norma Code 39 define un total de 44 caracteres: las 26 letras del alfabeto, los diez dígitos del "0" al "9" y los ocho caracteres especiales "*" (carácter de inicio/parada), espacio, "-", "+", ".", "/", "%" y "$".
Los códigos QR, formados por puntos sobre una superficie cuadrada, son una evolución de los códigos de barras. Son códigos bidimensionales y requieren una cámara para leerlos y descodificarlos.
¿Qué es el código Morse?
Uno de los primeros códigos "técnicos" utilizados para que las máquinas pudieran leer los caracteres fue el código Morse, desarrollado en 1838 por Alfred Vail (1807-1859), empleado de Samuel Morse (1791-1872), y normalizado por primera vez en 1865. El código Morse representa los números y las letras del alfabeto como secuencias diferentes de señales cortas ("Dit") y largas ("Dah"). Por tanto, puede utilizarse no sólo para la telegrafía eléctrica, sino también para otras señales, como señales luminosas, tonos o guiones de dos longitudes diferentes, y es, por tanto, completamente independiente de la tecnología de transmisión.
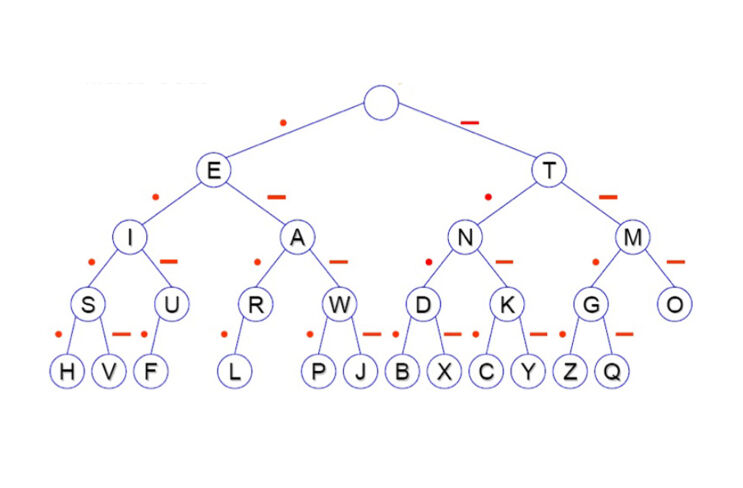
La codificación de las letras del alfabeto se muestra en el siguiente árbol de códigos. Una "E" se codifica con un "Dit", una "A" con un "Dit" seguido de un "Dah" y una "N" con un "Dah" seguido de un "Dit". Los caracteres del código son, por tanto, de distinta longitud.
Así pues, el código Morse tiene otra propiedad muy valiosa: es muy eficaz porque utiliza secuencias de señales cortas para las letras de uso frecuente y más largas para las raras, compensando así parcialmente la redundancia de las lenguas naturales.
La longitud de una "Dah" corresponde a la longitud de tres "Dit". Se envía una pausa de un "Dit" entre dos símbolos, una pausa de tres "Dit" entre dos letras de una palabra y una pausa de siete "Dit" entre dos palabras. La velocidad de transmisión viene determinada por la longitud de un "Dit".
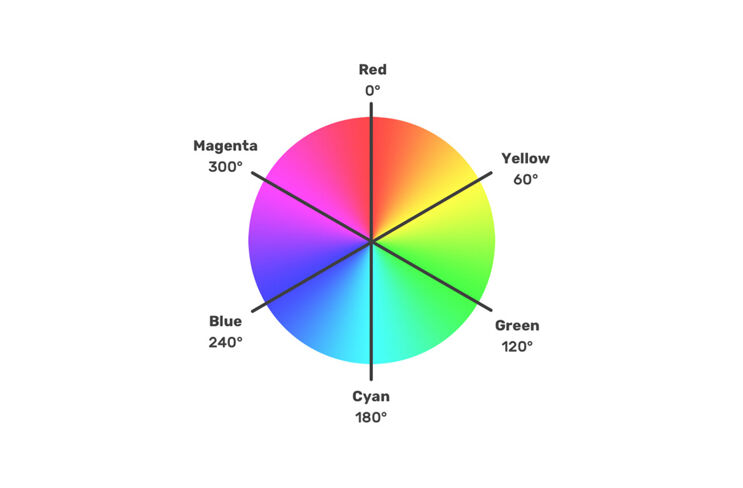
¿Cómo funciona el código de color RGB?
El código RGB es una codificación de tres bytes de los componentes de color R (rojo), G (verde) y B (azul, cada uno de 0-255) en un tono. El tono de color (matiz) puede determinarse a partir de un valor RGB de la siguiente manera:
Determina el máximo Max:=max(R, G, B) y el mínimo Min:=min(R, G, B)
Calcula la diferencia Diff:=Max-Min
Si Diff > 0
Si Max = R: Tono := (G-B)/Diff
Si Max = G: Tono := 2+(B-R)/Diff
Si Max = B: Tono := 4+(R-G)/Diferencia
Tono := Tono/6
Si Tono < 0: Tono := Tono + 1
Ángulo del círculo cromático: Ángulo := Tono - 360
El resultado es el ángulo en el que se encuentra este color en la rueda cromática (véase la ilustración).
¿Qué es la redundancia?
En teoría de la información, la redundancia se refiere a los datos que pueden omitirse sin pérdida de información. Un código es redundante si requiere más bits que el mínimo necesario para representar los distintos caracteres. Si todos los caracteres del código tienen la misma longitud, el número de bits adicionales del código que no son realmente necesarios para la representación de la información indica su redundancia. Por ejemplo, si queremos codificar una simple señal 1/0, sólo necesitamos un bit. Sin embargo, si codificamos la señal con los dígitos "1" y "0" (como caracteres ASCII), nuestro código requiere ocho bits. Por tanto, la codificación tiene una redundancia de siete (bits):
Redundancia = log₂ (número de palabras de código posibles/número de caracteres a codificar).
En nuestro ejemplo, la redundancia es, por tanto, log₂ (2⁸/2) = log₂ (2⁷) = 7.
¿Cómo funciona la encriptación?
La encriptación de datos (también conocida como cifrado) se utiliza para mantener en secreto el contenido de un mensaje entre el remitente y el destinatario e impedir que lo "lean" personas no autorizadas. Para ello, se utilizan métodos de cifrado que "modifican" el mensaje de una manera acordada entre el emisor y el destinatario. En la medida de lo posible, no se mantiene en secreto el método de cifrado en sí, sino una clave que sólo conocen el emisor y el destinatario ("principio de Kerkhoff"). En la mayoría de los casos, los caracteres del mensaje se reemplazan (sustituyen) o intercambian (permutan).
En el pasado, se utilizaban principalmente cifrados de sustitución simples. Uno de los métodos más conocidos es el llamado "cifrado César". Consiste en "desplazar" las letras del mensaje que se quiere transmitir en el alfabeto un número fijo de dígitos (la clave). Por ejemplo, con la clave "3", una "A" se convierte en una "D", una "B" en una "E" y así sucesivamente, hasta que una "Z" se convierte finalmente en una "C". El descifrado en el extremo del destinatario es exactamente lo contrario.
El cifrado César es fácil de descifrar porque la distribución de frecuencias de las letras en un lenguaje natural no cambia con el cifrado: En un texto largo, la letra más frecuente con diferencia es la "E". Si se conoce la letra más frecuente del texto cifrado, se sabe cuántos lugares hay que "desplazar" en el alfabeto para descifrar el texto escuchado.
Además, sólo hay 25 formas distintas de desplazar las letras del alfabeto: Es un número muy pequeño de claves posibles. Por lo tanto, se pueden probar distintos desplazamientos hasta que, al descifrar, aparezca un texto con sentido.
Un cifrado publicado por Blaise de Vigenère (1523-1596) en 1586, en el que los caracteres del mensaje no se desplazan todos el mismo número de lugares en el alfabeto, sino según un esquema predeterminado, es mucho más difícil de descifrar. Por ejemplo, la clave "1 5 12 4 8 7 11" significa que el primer carácter del mensaje se desplaza un lugar, el segundo cinco, el tercero 12, etc. y, por último, el séptimo 11 lugares en el alfabeto. El octavo carácter se desplaza de nuevo uno, el noveno cinco y así sucesivamente. El método de cifrado de Vigenère se consideró indescifrable durante casi trescientos años.
A menudo, la clave no está representada por una secuencia de números, sino por las letras correspondientes del alfabeto: en el ejemplo anterior, por "AELDHGK". Esto también facilita mucho la programación de la sustitución de los caracteres ("sumando" las posiciones en el alfabeto).
¿Qué es un controlador?
A diferencia de un control por microcontrolador, en el que un actuador se ajusta a un valor predefinido (por ejemplo, un LED a un valor de luminosidad o un motor codificador a una posición determinada), un controlador garantiza automáticamente el mantenimiento de un valor de consigna incluso en caso de fallos (por ejemplo, un seguidor de vía continúa siguiendo la vía incluso en una curva).
Para ello, el controlador necesita un mecanismo de "realimentación" que le informe si se producen desviaciones respecto a la magnitud de referencia especificada. Un controlador puede representarse esquemáticamente como se muestra en el siguiente diagrama:
Si la variable controlada se desvía de la variable de referencia (la especificación), el controlador corrige cambiando una variable manipulada para reducir la desviación. Por ejemplo, si se desea mantener constante el número de revoluciones de un eje motorizado por unidad de tiempo incluso con una carga cambiante, hay que medir las revoluciones y aumentar o disminuir la tensión del motor en caso de desviaciones.
Con el control en bucle cerrado, hay varias formas de incorporar la desviación al cambio de la variable manipulada: En el caso de un controlador proporcional (también controlador P), por ejemplo, la corrección se realiza en proporción a la magnitud de la desviación. Si el regulador se excede, es decir, si un efecto retardado de la regulación hace que la corrección tarde demasiado tiempo, la regulación puede amortiguarse con un elemento diferencial adicional (también conocido como elemento D), que tiene en cuenta la variación de la desviación. Esto amplifica el control en caso de una perturbación fuerte y repentina y lo atenúa en caso de una disminución rápida de la desviación.
Un regulador integrador (regulador I o elemento I) también tiene en cuenta la duración de la desviación incorporando la suma de las desviaciones medidas a la corrección y acelerando así la aproximación al valor deseado.
A la hora de diseñar un controlador adecuado, el mayor reto consiste en determinar los factores por los que deben multiplicarse los valores que se incluirán en el control (desviación, cambio en la desviación, suma de desviaciones) para conseguir el efecto de control deseado. A menudo se consigue más rápidamente mediante la experimentación. Normalmente, se empieza determinando el factor para el elemento P y se selecciona de forma que el regulador no oscile (es decir, que disminuya el sobreimpulso). A continuación, se añade el factor para el elemento D y se empieza con un factor muy pequeño, que se aumenta lentamente hasta que la respuesta transitoria a la variable de referencia es lo suficientemente rápida.
Con el elemento I, es importante asegurarse de que los valores de las desviaciones no se totalizan permanentemente (por ejemplo, sólo se tiene en cuenta un número limitado de desviaciones pasadas o se reduce el valor total antiguo, por ejemplo, dividiéndolo por un valor constante, antes de añadir la siguiente desviación), ya que, de lo contrario, el elemento I dominará muy rápidamente los componentes P e I.
Un regulador con componentes P, D e I también se conoce como regulador PID.
Descarga la ROBO Pro Coding App
Antes de que puedas empezar, necesitas descargar la ROBO Pro Coding App. Simplemente selecciona el sistema operativo apropiado y haz clic en el enlace:
Descargar la Voice Control App
¡Dile al robot dónde tiene que ir! Sólo tienes que descargar nuestra aplicación Voice Control y darle al robot órdenes personalizadas:
